|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Jovian Moons Applet
| The Galilean
moons are the four moons of Jupiter discovered by
Galileo Galilei in January 1610: Io, Europa,
Ganymede and Callisto. They revolve around Jupiter with periods of 1.77 to 16.69 days, and have apparent magnitudes between 4.6 and 5.6 when Jupiter is in opposition with the Sun, and are about one unit of magnitude dimmer when Jupiter is in conjunction. |
|
|
Check your time zone offset and select the local standard time. |
|
|
Click the applet first! 52.51° N, 13.41° E is Berlin, Germany. |
|
|
You may use the keys "m", "d", "h", "n" to increase the month, date, hour, minute, or Shift key and "m", "d", "h", "n" to decrease the month, date, hour, minute ! |
 |
The sizes of
the moons are drawn according to their visual
magnitudes (accuracy about +/- 0.1 mag). The angular distances from Jupiter, and the angle from inferior conjunction are at right. |
 |
With "Orbit"
selected from the "View" menu the illumination of
Jupiter can be shown. |
 |
The radii of
Jupiter and the orbital radii of the satellites are
drawn to scale. |
 |
Blue: Jupiter
visible in the local sky. |
| The
simplified calculations used by the applet (according
to Jean Meeus: Astronomical Algorithms) is neglecting
the inclinations of the orbits of the satellites on
the equatorial plane of Jupiter (0.04° for Io, 0.51°
for Callisto): mutual occultations can not be
calculated with certainty. For 1610 the accuracy of times of inferior conjunctions of Callisto was tested by comparison with CalSky, and the deviations were found to be less than 2 minutes. |
|
Orbital period of the Galilean moons:

Select "Diagram Moons" from the "View" menu:
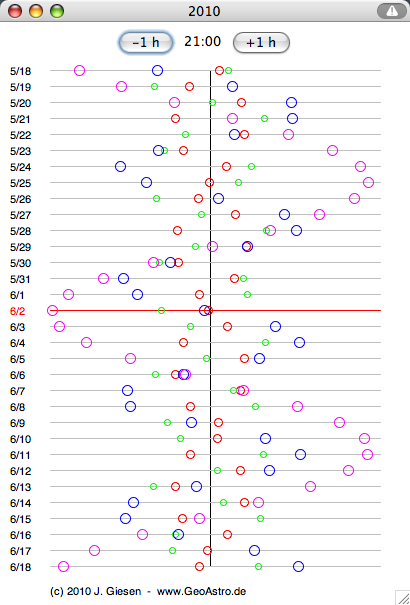
Select
"Ecliptic Plane" from the "View" menu:
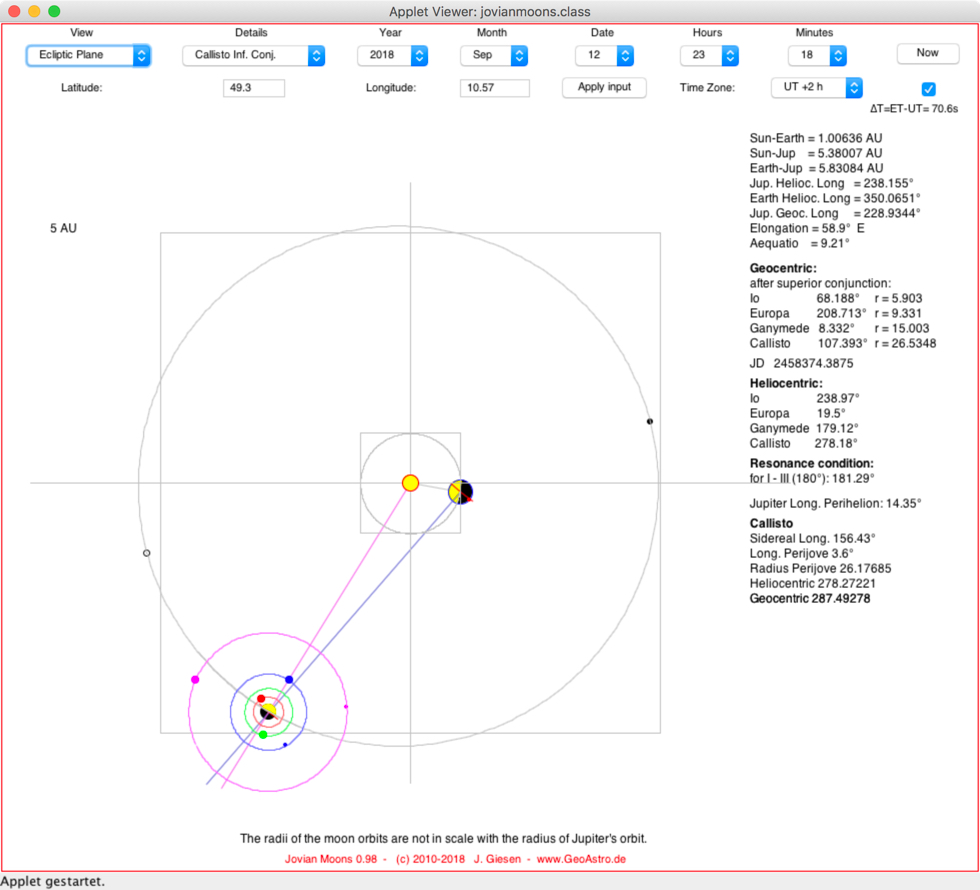
The three
inner moons—Io, Europa, and Ganymede—are in a 4:2:1 orbital
resonance with each other.
The Laplace resonance involving Io–Europa–Ganymede includes
the following relation locking the orbital phase of the moons:
λ are mean longitudes of the moons. This relation makes a triple conjunction impossible. (from Wikipedia)
The relation was found by Laplace.
Details
Select "Sky"
from the "View" menu:
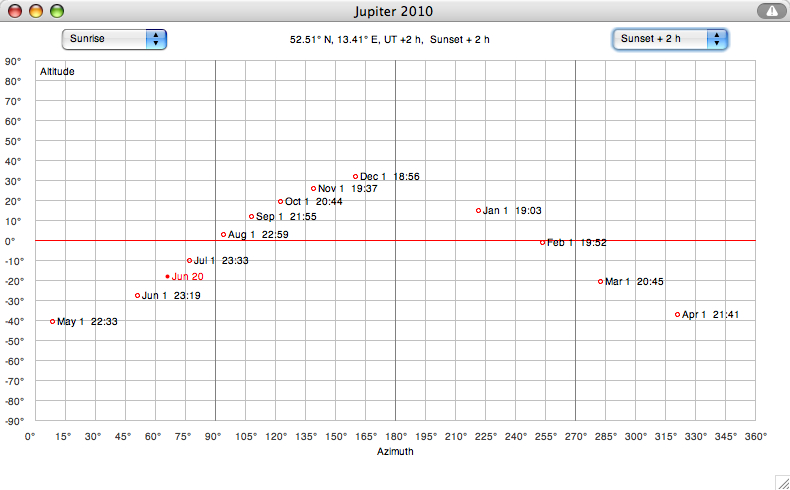
Jupiter's
altitude
and azimuth on the first of the month, 2 hours after sunset
Extreme
visual magnitudes of the Galilean Moons:
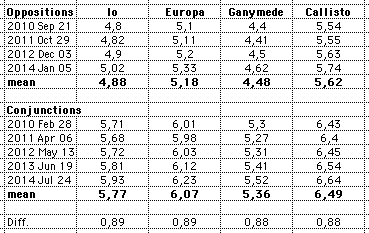
Extreme
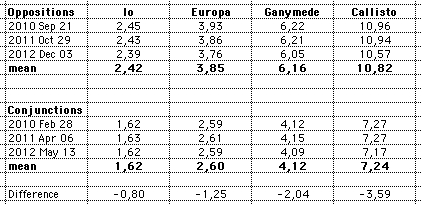
angular distances of the Galilean Moons from Jupiter (arc
minutes):
The discovery of the Galilean moons
Galilei's observations of
1610 January at Padova (45.4° N, 11.9° E) were published in
"Nuncius Sidereus"
in Venice in March 1610.
The
year
1610 can be selected from the "Year" menu:
Jan 07:
Sunset 15:47 UT

Credit:
Linda Hall Library of Science, Engineering and Technology,
[Page 17 [sic].]*
Simulation at 17:00 UT:

Jan 08:
Callisto missing

Credit:
Linda
Hall
Library
of
Science,
Engineering
and Technology, [Page 18 [sic].]*
Simulation at 17:00 UT:

Jan 10:

Credit: Linda Hall Library of Science, Engineering and
Technology, [Page 18 [sic].]*
Simulation at 17:00 UT:

Jan 13:

Credit:
Linda
Hall
Library
of
Science,
Engineering
and Technology
Simulation at 17:00 UT:

Sufficient
separation
for Galilei's perspicillum to observe four moons.
Jupiter seen without moons:
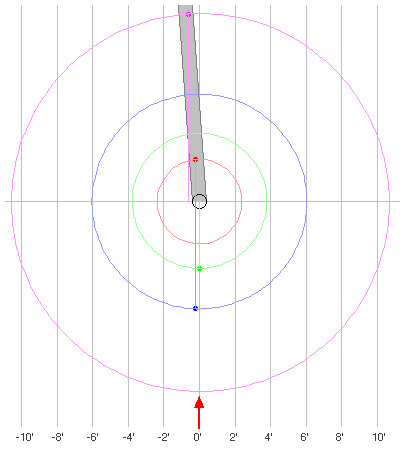
2009 Sep 3, 5:30 UT:
Io occulted/eclipsed,
Europa and Ganymede in transit,
Callisto in eclipse/transit.
Next event: 2019 Nov 9
Jupiter seen with one satellite
only:
This event is occurs far more frequently.
2010
Mar
19 at 14:00 UT:
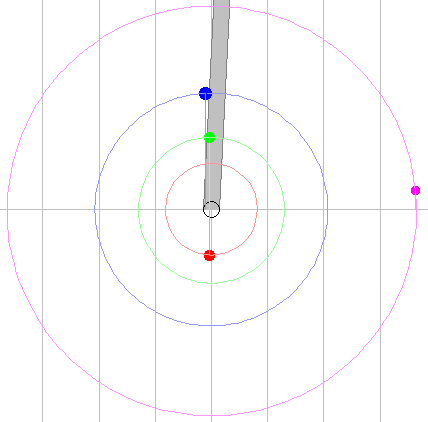
Io transit, Europa occulted/eclipsed, Ganymede
occulted.
2010
Oct
27 at 15:00 UT:
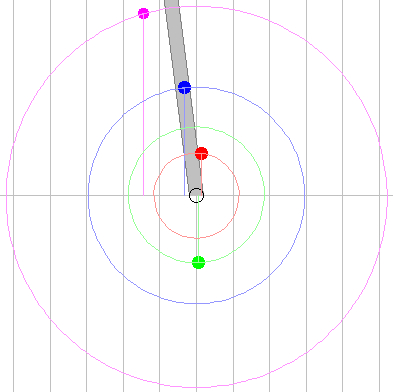
Io
occulted, Europa transit, Ganymede eclipse.
Orbital Periods as published by Simon Marius in 1614
| Simon
Marius |
Wikipedia |
Diff. |
||
| (I) Io |
1 d 18 h 28 min 30 s |
= 1.7698 d |
1.76914 d |
1 min 0.2 s = 0.04 % |
| (II) Europa |
3 d 13 h 18 min |
= 3.5542 d |
3.55118 d |
4 min 16 s = 0.08 % |
| (III) Ganymede |
7 d 3 h 56 min 34 s |
= 7.1643 d |
7.15455 d |
3 min 57 s = 0.14 % |
| (IV) Callisto |
16 d 18 h 9 min 15 s |
= 16.75642 d |
16.68902 d |
1 h 37 m = 0.40 % |
| Books |
| Simon Marius: Mundus Jovialis -
Die Welt des Jupiter - Die Entdeckung der Jupitermonde
durch den fränkischen Hofmathematiker und Astronimen
Simon Marius im Jahr 1609 - lateinisch und deutsch. Herausgegeben und bearbeitet von Joachim Schlör, Schrenk-Verlag, Gunzenhausen, 1988. ISBN 3-924270-14-7 Wolfschmidt, Gudrun (Hg.): Simon Marius, der fränkische Galilei, und die Entwicklung des astronomischen Weltbildes. Tredition, Hamburg 2012. ISBN 978-3847238645 Galileo Galilei: Sidereus Nuncius - Nachricht von neuen Sternen. Hg. Hans Blumenberg, Suhrkamp 1980. ISBN 978-3518279373 |
|
|
|
The Mundus Jovialis of Simon Marius: Jovian Satellite Fact Sheet (NASA) Jovian system simulator (high accuracy) Jupiter's Moon (simulation, Sky &
Telescope) Phenomena
of the Galilean Satellites of Jupiter (IMCE) Galilei: Nuncius Sidereus (Linda
Hall
Library of Science, Engineering and
Technology) From
Occhiale
to Printed Page: The Making of Galilei's Nuncius
Sidereus Jupiter satellite events and GRS
times for 2012-2013 Orbital
resonance (Wikipedia) Paita,
F. et al.: Element history of the Laplace
resonance: a dynamical approach Laplace,
P.-S.: Traite de Mecanique Celeste Vol. IV,
Paris 1805, chez Courcier. |
Last Modified: 2023, Oct 05
© 2010-2023 Juergen Giesen
![]()
