|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Transit and Culmination
|
The culmination
of a celestial body means that the body is at
its greatest altitude, whereas the transit
is the
passage of its center through the meridian.
Only the fixed stars culminate really in the meridian. The Sun, Moon, and the planets culminate out of the meridian. At mid-latitudes (50°) the difference may be up to 18 seconds for the Sun, and more than 6 minutes for the Moon. To compute the difference in time between transit and culmination we start by the well known equation 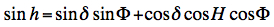 (1)
(1)
h = altitude
δ = declination Φ = latitude H = hour angle = Local Sidereal Time - Right Ascension Differentiating the above equation with respect to time: 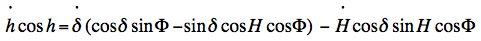 (2)
(2)
At
the instant of culmination we have
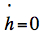 .
If .
If 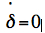 (constant declination) the culmination
is at H=0°.
(constant declination) the culmination
is at H=0°.For non constant declination the hour angle of culmination HC is very small 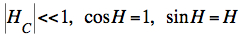 and we get as an
approximation of (2):
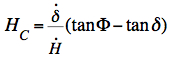 (3)
(3) The altitude at
culmination is by
∆h
greater
than the
altitude on the meridian:
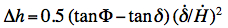 (4)
(4)
In
(3) the
derivative
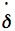 may
be replaced by differentiating the
classical equation may
be replaced by differentiating the
classical equation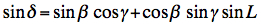 (5)
(5)
β = ecliptic latitude
γ = obliquity of the ecliptic L = ecliptic longitude 1. The Sun
The
ecliptic latitude β of
the Sun is very small:
| β
|<0.0002°,
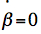 , cos
β=1, and
therefore from (5): , cos
β=1, and
therefore from (5):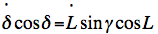 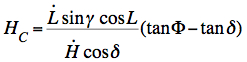 (6)
(6)
L =
heliocentric ecliptic longitude
H = hour angle = Local Sidereal Time - Right Ascension γ = obliquity of the ecliptic = 23.44° δ = declination Φ = latitude For the Sun the rates of change in time (derivatives) of L and H in (6) can be approximated by: (0.986
°/d<
(358.6 °/d< For equinoxes
(δ=0°,
L=0°, L=180°) HC
is an extremum:
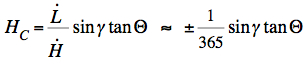 (7)
(7)
At Φ = 40°
we get HC =
9,14·10-4 rad = 0,0524° = 0.210 min
= 12.6 s
At Φ = 50° we get HC = 1,30·10-3 rad = 0,0744° = 0.298 min = 17.9 s The altitude of the Sun at culmination is 0.14'' higher than at transit, only 1/13000 of it's diameter, very difficult to measure ! Between transit and culmination the Sun moves 1/5.5 of it's diameter. The effect is of no visual consequence. In polar
regions there is a maximum:
At
Φ = 85° we have HC
= 172 s, at
Φ = 87,5° we
have HC
= 345 s !
For summer and winter solstice
(L=90°,
L=270°)
culmination occurs precisely at meridian
passage:
HC
= 0 s.
Between winter solstice and summer solstice culmination occurs later than transit, between summer solstice and winter solstice culmination occurs earlier than transit. 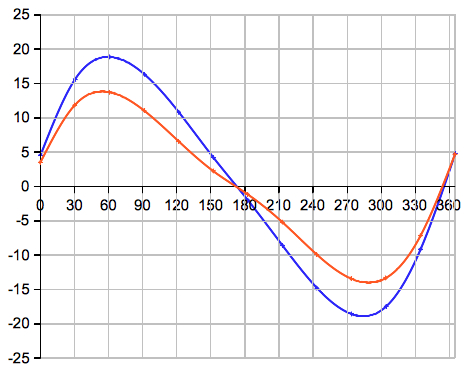 horizontal
axis: day of the year
vertical axis: time difference in seconds between culmination and transit red: latitude Φ = 40°, blue: latitude Φ = 50°. ∆T = (48/PI)*(tanΦ-tanδ)*(vLat-vDec) (8) On 2012,
Mar 20 at 05:14 UT (spring equinox):
∆T =
18.0 svLat = latitude speed is arcminutes per hour = 0 (observer at rest) vDec = hourly declination change  is arcminutes per hour = -0,988 arcmin/hour
is arcminutes per hour = -0,988 arcmin/hourδ = 0.0° at Φ = 50°: This
result agrees with (7).
Using my spreadsheet to compute ∆T by formula (6), but inserting the dayly value of on 2018, Jan 1 at 40°N, 0°E I get the result: ∆T = 4.06 s
Evaluating the data of JPL HORIZONS Web Interface
(apparent AZ and EL) results:
∆T = 4.07 s
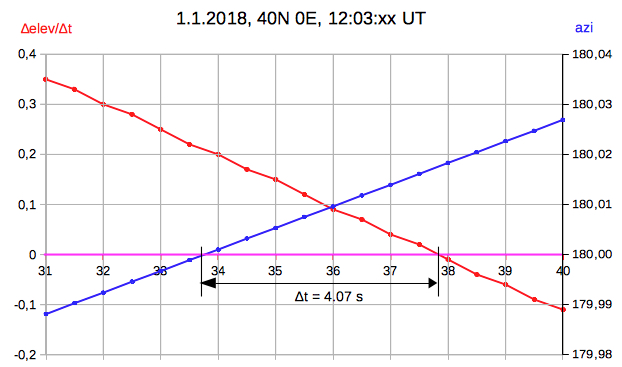 Comparing JPL and
spreadsheet results for azimuth and
refracted elevation:
Date__(UT)__HR:MN:SC.fff Azi_(r-apprnt)_Elev ******************************************************************** $$SOE 2018-Jan-01 12:03:00.000 * 179.85467 27.05276 Spreadsheet
latitude 0°:
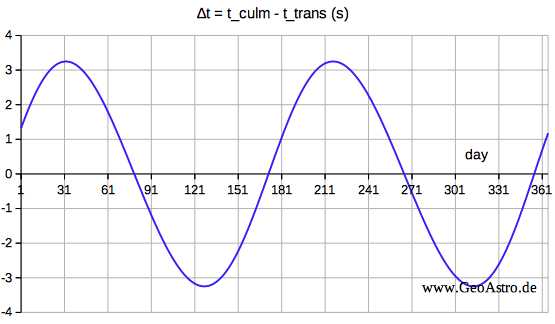 Using
formula (4) for ∆h=h_culm - h_trans and the
approximation
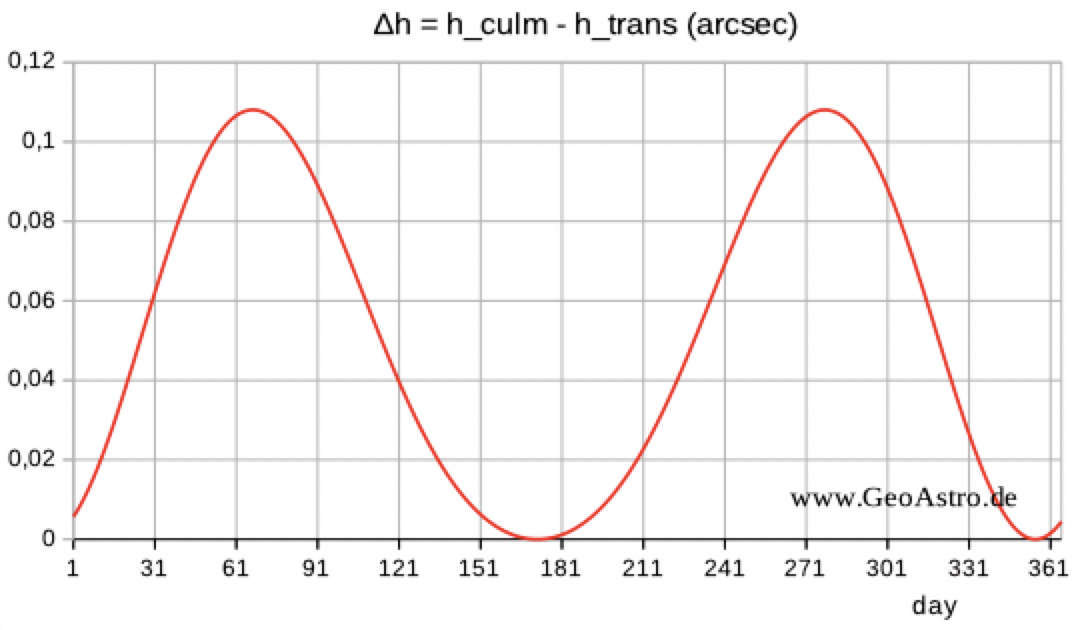 The
difference in elevation ∆h is less than 0.11 ''.
The results of my spreadsheet for
2018, Mar 1 are:
∆T=14.1 s and ∆h=0,106 ''.
Comparing with JPL
HORIZONS
Web Interface data:∆T=14.1 s
mean
dElev/dt=0.475 ''/min between transit
and culmination:∆h=0.112 ''
The difference in azimuth between
culmination and transit is 0.08°.
*************************************2. The Moon The
orbital plane of the Moon is inclined (|
β
|< 5.1°)
against the ecliptic, and formula (6) is not
valid.
a. Stellarium,
a free planetarium, is quite comfortable to
get the difference in time ∆T between transit
and culmination, as well as the difference in
elevation, and azimuth.
On 2024, Oct 15 there is a large value of ∆T. At 50°N, 0°E: Transit (local time):
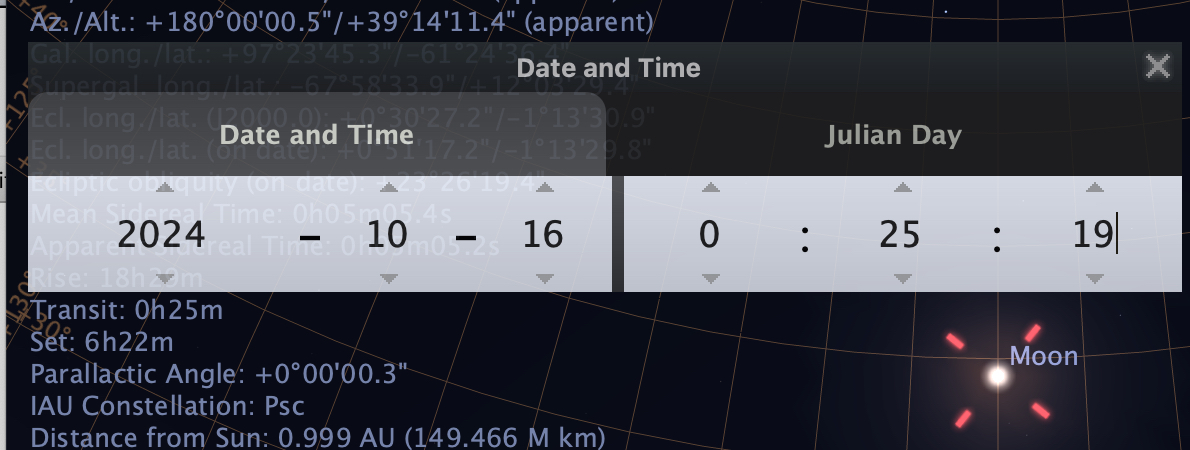 Culmimation (local time):
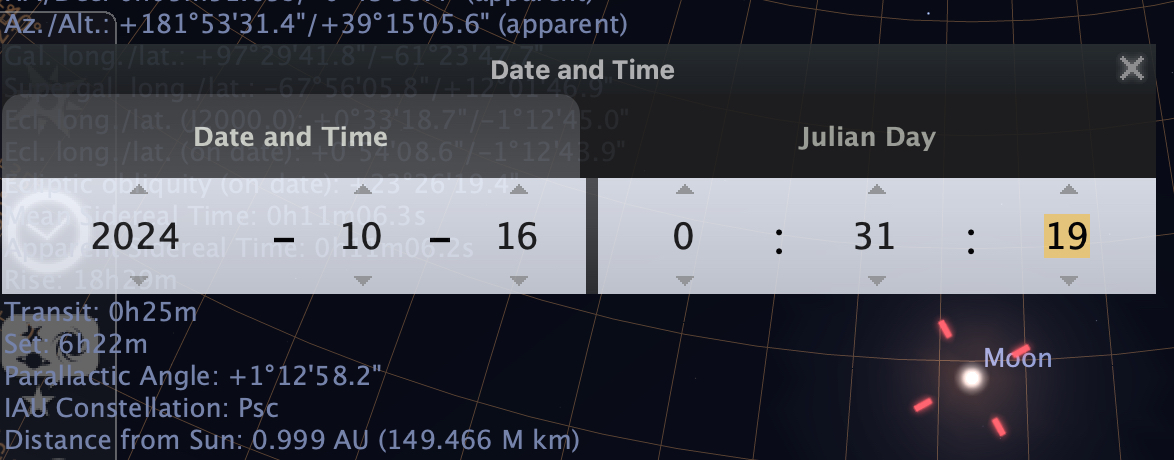 Result: ∆T=360 s, ∆h=-0.903
arcmin, ∆az=-1,89°
*****
b.
My spreadsheet
is
most comfortable: computing the elevation
and azimuth of the Moon every 30 minutes
of a day, and evaluating the data to get
∆T, ∆h, and ∆az by a few key strokes to
insert the date.It's made by LibreOffice
6.3.6.2 for MAC (.ods file). Saved as .xls
file it can be opened by Excel.
Example: 2024, Oct
15, at 50°N, 0°E:
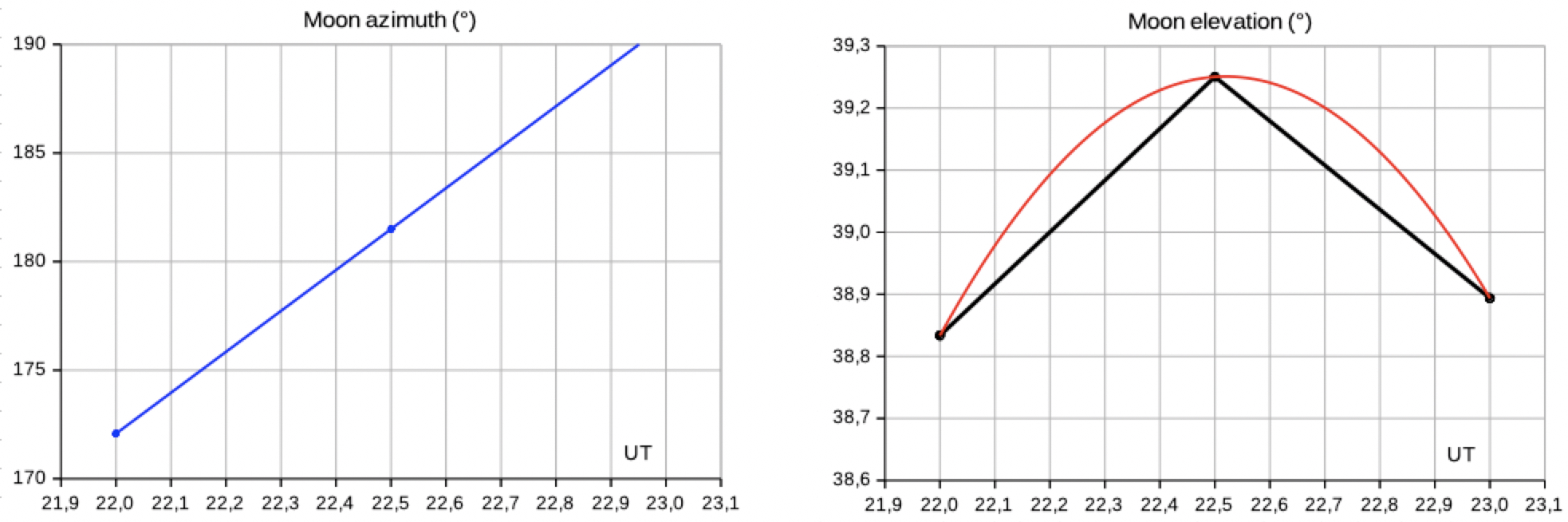 The numerical
results by quadratic (elevation) and
linear (azimuth) interpolation:
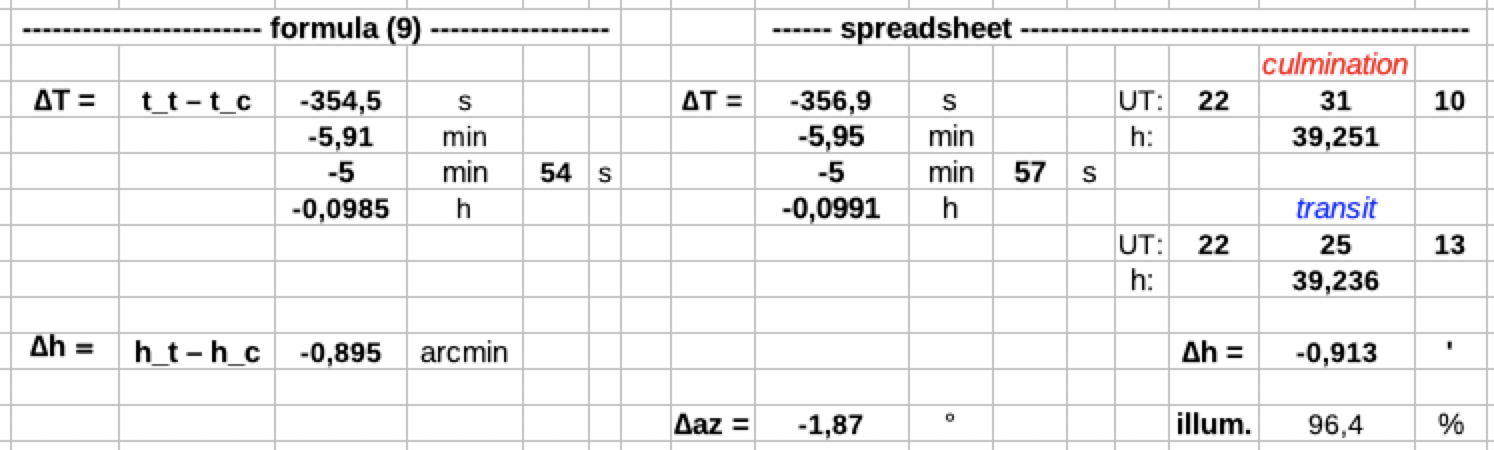 ∆T
= 360 s = 6 min 0 s, ∆h
= -0.93 arcmin, ∆az = -1.87°
c. On 2024, Oct 15 at 50°N, 0°E (computed by MICA, Multiyear Interactive Computer Almanac by USNO): culmination 22:31:14.5 UT transit 22:25:19.3 UT difference 5 min 55 s d. The result from CalSKY is 6 min 03 s. e. On
2024, Oct 15 at 22:30 UT we apply the formula
(3) for the Moon using MICA:
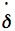 = dδ/dt
= 0.303°/hour
= dδ/dt
= 0.303°/hourdH/dt = 14.56°/hour δ = 0.00° HC = 0.0248 rad = 1.42° = 5.68 min HC
= 5 min 41 s
∆T = [10800°/(PI*(dH/dt)2)]*(tanΦ-tanδ)*(vLat-vDec) (9) ∆T =
difference is seconds of time between
culmination and meridian transit
∆H/dt = hourly change of hour angle, H in degrees vLat = hourly latitude speed of the observer is arcminutes per hour For the Moon: 14.38°/hour
< dH/dt
<
14.61°/hour
mean: 14.495°/hour = 360°/24h 50min 16.105
hour2/° < 10800°/[PI*(dH/dt)2]
<
16.625 hour2/°
mean: 10800°/[PI*(dH/dt)2] = 16.365 hour2/° On 2024, Oct 15 at 22:30 UT using MICA: vLat = 0 (observer is at rest) vDec = hourly declination change 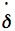 in arcminutes per hour
= 18.19 arcmin/hour in arcminutes per hour
= 18.19 arcmin/hour=(18.19/60) °/hour δ = 0.025° dH/dt = 14.49°/hour 10800°/[PI*(dH/dt)2] = 16.37 hour2/° = 16.37 hour·60 s/° ∆T =
355 s = 5 min 55 s
******************
Summary 2024, Oct 15 at 50°N, 0°E
******************
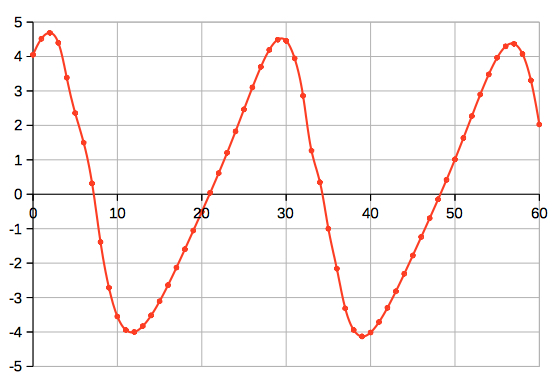 Vertical axis: Difference ∆T = tTrans - tCulm (minutes) at 50°N horizontal axis: day in May-Jun 2012 computed by my Planet applet Urs Klaeger pointed out to me: With increasing declinations AND at geo-latitudes north of the subsolar/sublunar point, Culmination is after Transit. Vice versa south of the Sun/Moon. Jean Meeus writes: If culmination occurs south of the zenith and ∆δ is positive, the highest altitude is reached after the meridian passage; if the culmination occurs between the pole and the zenith, the situation is reversed. („More Mathematical Astronomy Morsels“, page 320) 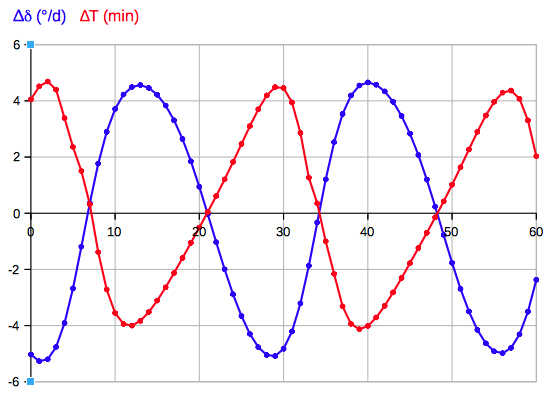 Moon at 50°N, May-Jun 2012: daily change of declination (∆δ), and ∆T = tTrans - tCulm (minutes) e.g. on
May 10:
∆δ>0, and ∆T<0: culmination is after transit. 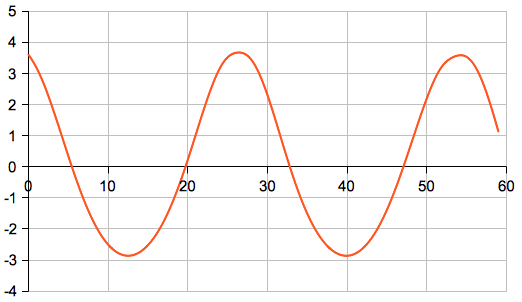 Vertical axis: Difference tTrans - tCulm (minutes) at 50°N 0°E horizontal axis: day in Sep-Oct 2015 computed by my Planet applet 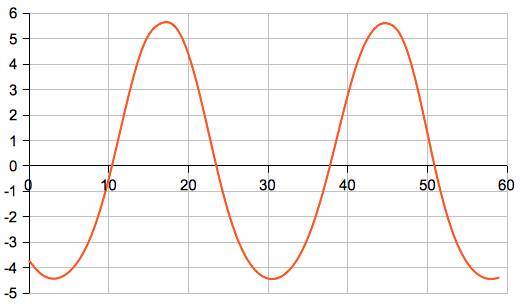 Vertical axis: Difference tTrans - tCulm (minutes) at 50°N 0°E horizontal axis: day in Sep-Oct 2024 computed by my Planet Applet It seems that the
variation of ∆T is dominated by the
18.6-year cycle of lunar
standstills:
small values of ∆T (up to 4 minutes) are occuring in years of minor lunar standstills (1996, 2015), and large values (more than 6 minutes) in years of major lunar standstills (2006, 2024/2025). Max. declination in 2024 on Sep 24 at 17 UT: 28.70° Min. declination in 2024 on Oct 09 at 12 UT: -28.70° Change in declination: -14.22 arcmin/h < Max. declination in 2015 on Jan 03 at 18 UT: 18.65° Min. declination in 2015 on Jan 18 at 06 UT: -18.58° Change in declination: -9.42 arcmin/h < 2006 (major lunar
standstill) Aug 10, 50°N, 0°E
transit
00:40:34 UT MICA:
culmination 00:46:48 UT ∆T = 6 min 14 s Planet Applet: transit 00:40:34 UT culmination 00:46:49 UT ∆T = 6 min 15 s calsky:
transit:
00h 40m 34.2s UT
culmination:
00h 46.9m UT
∆T = 6 min 20 s StarryNight SN7 CSAP transit: 00h 40m 34.2s UT culmination: 00h 46.8m UT ∆T = 6 min 15 s The altitude at culmination is only 0.81' more than at transit. by formula (3) and MICA: 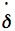 = dδ/dt =
-0,2585°/hour
= dδ/dt =
-0,2585°/hourdH/dt = 14.45°/hour δ = -15.55° ∆T = 6 min 02 s 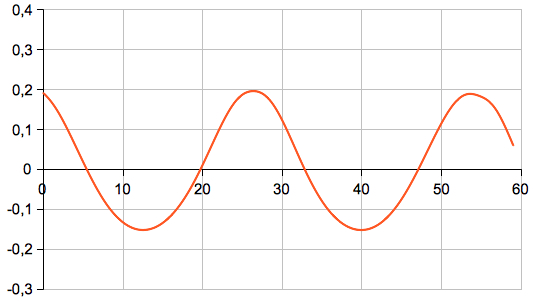 Vertical axis: hourly change of Declination (degrees) horizontal axis: day in Sep-Oct 2015 minor lunar standstill  Vertical axis: hourly change of Declination (degrees) horizontal axis: day in Sep-Oct 2024 major lunar standstill The result by formula (3) or formula (8) will be large for northern latitudes, if δ<0, and if |  |is large. dH/dt is
nearly constant (14.38°/hour to
14.61°/hour). |is large. dH/dt is
nearly constant (14.38°/hour to
14.61°/hour).3. The Planets As an example
transit and culmination of Mars at
50°N, 0°E:
Mars, 2012 May 25 (computed by
MICA):
Transit
18:41:50
UT, 18:41:51.2 UT
Culmination 18:41:43 UT, 18:41:45 UT ∆T = 7 s Mars, 2012 May 25 (computed
by StarryNight):
Transit
18:41:50
UT, 18:41:51.2 UTCulmination 18:41:43 UT, 18:41:44.5 UT ∆T = 6,7 s Mars, 2012 Aug 01 (computed by MICA): Transit 16:17:38 UT Culmination 16:17:26 UT ∆T = 12 s Mars, 2012 Aug 01 (computed by StarryNight): Transit 16:17:38 UT, 16:17:40.7 UT Culmination 16:17:26 UT, 16:17:28.5 UT ∆T = 12.2 s Mars, 2013 Apr 01 (computed by MICA): Transit 12:18:19.5 UT Culmination 12:18:32 UT ∆T = 12.5 s, ∆h = 0.07 '' Mars, 2013 Apr 01 (computed by StarryNight): Transit 12:18:20 UT, 12:18:22.9 UT Culmination 12:18:34 UT, 12:18:36 UT ∆T = 13.1 s Mars, 2020 Oct 13 (computed by Stellarium): Transit 23:50:25 UT Culmination 23:50:22 UT ∆T ≈ 3 s
Table from Wilson 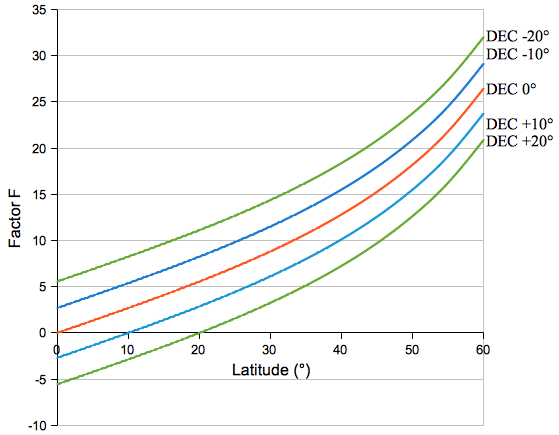 Using the diagram
above to get ∆T for the Sun, look up the
value of F (depending on latitude
and declination), and multiply F
by the hourly
declination change
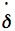 in arcminutes per hour: in arcminutes per hour:Φ = 50°, δ = 0°, F = 18, 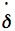 = 1 arcmin/h, ∆T = 18 s = 1 arcmin/h, ∆T = 18 s***
A paper by
Pio (1899) describes the
determination of the longitude (at known
latitude) from the culmination of the Moon:
The instants of two equal altitudes are
measured by a chronometer and a sextant, and
the time of culmination is "reduced to the
meridian". The practical advantage of the
method is that it does not require any transit
instruments.
*********************************
4.
International Space Station
At CalSKY I
found for my location
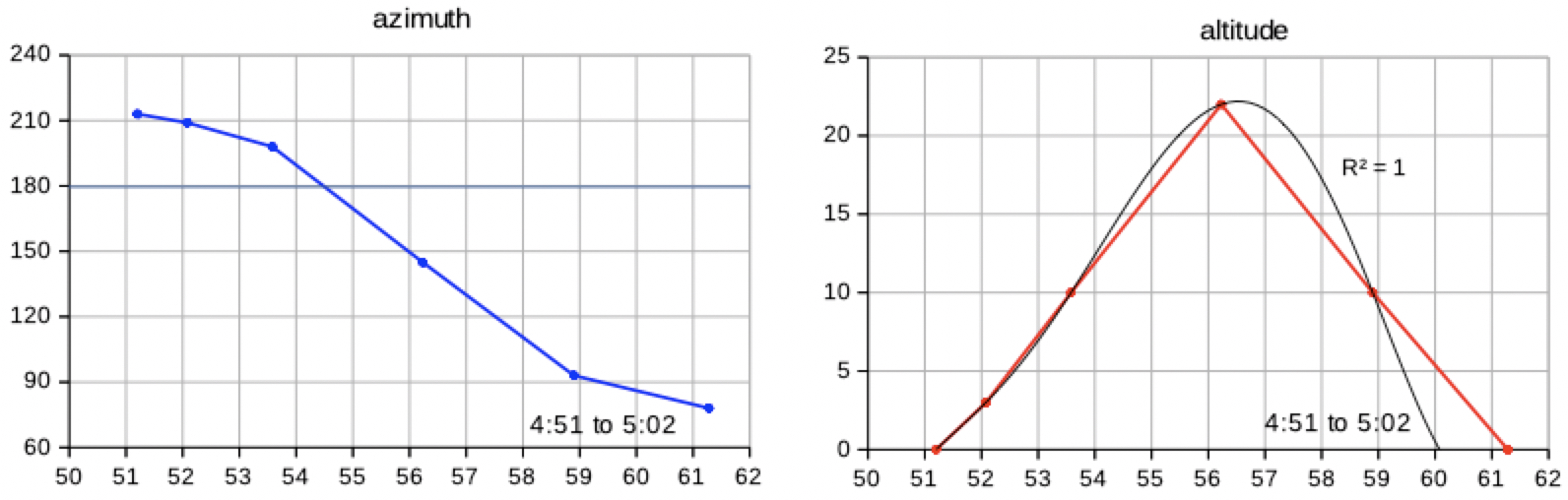
Lon: +7d58m00.00s Lat: +51d37m00.00s Alt: 122m Tuesday, 30 June 2020 ISS Appears 4h53m36s -1.1mag az:211.1° SSW h:2.8° at Meridian 4h56m36s -2.3mag az:180.0° S h:17.6° Culmination 4h57m57s -2.3mag az:145.7° SE h:22.5° distance: 953.4km height above Earth: 421.4km elevation of Sun: -2° angular velocity: 0.47°/s Disappears 5h03m01s 2.0mag az: 77.5° ENE horizon Time uncertainty of about 2 minutes For the difference between
transit (meridian) and culmination:
∆T = 1m 21s, ∆h = 4.9°, ∆az =
34.3°
*** 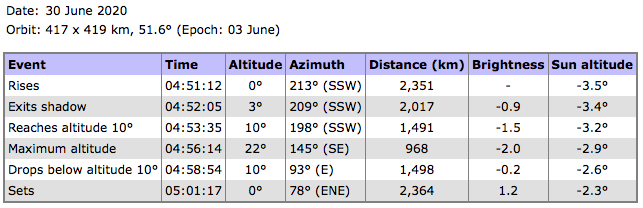 Evaluating the table results:
∆T = ∼ 2m, ∆h
= ∼ 7°, ∆az
= ∼
45°
 |
|
|
| D. A. Pio: Longitude from the Moon
Culminations, Monthly Notices of the Royal
Astronomical Society, from November 1998 to
November 1999, Volume LIX, London 1899. [NavList 9938] Re: Time of meridian passage accuracy James N. Wilson: Position from Observation of a Single Body (Appendix I) |
| Books |
| Jörg
Meyer: Die Sonnenuhr und ihre Theorie, Verlag
Harry Deutsch, Frankfurt 2008, ISBN 978-3817118243 Jean Meeus: More Mathematical Astronomy Morsels, Willmann-Bell, 2002, ISBN 978-0943396743 |
| Software |
| MICA Multiyear
Interactive Computer Almanac 1800-2050 by
U.S. Naval Observatory (Willmann-Bell) StarryNight 7 CSAP |
![]()
(c)
2012-2023 J. Giesen
Last update:
2023, Oct 07