Free Fall without and with Air Resistance
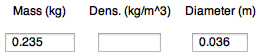 |
Enter mass (kg), and diameter (m) of the
body, |
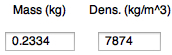 |
or enter mass (kg) and density (kg/m^3), e.g. 7874 kg/m^3 for iron, diameter will be computed |
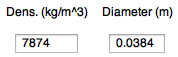 |
or enter density (kg/m^3), and diameter
(m), e.g. 7874 kg/m^3 for iron, mass will be computed |
 |
Enter acceleration (m/s^2), density of the
air (kg/m^3), drag coefficient (dimensionless), for a sphere the dag coefficient is cD = 0.4 .. 0.5 (0.47) |
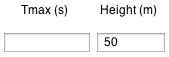
| enter maximum time (s), or Height (m), and press button "Apply Input" |
|
You may also use the Parachute mode: |
|
 |
Enter time (s), or Height (m), and press button "Apply Input". |
| Using mass = 150 kg, diameter = 9 m, drag coefficient cD = 1.3, dome-shaped chute cD = 1.3 .. 1.5, parasheet (flat sheet) cD = 0.75 the rate of descent will be about 5 m/s. |
|
| Using a "Height" input the delay due to air resistance is computed (∆t absolute, and ∆t/T in relation to the time T of free fall). | |
|
Theory
The equations without air resistance are quite simple. We assume g=const, s(t=0)=0, and v(t=0)=0: 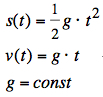 Taking into account the air
resistance force (drag force):
the equation of motion is The air resistance force
will increase until it equals the
gravitational force m.g, and
the body will then move at a constant
velocity vlimit as the net
force is m.a=0
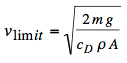 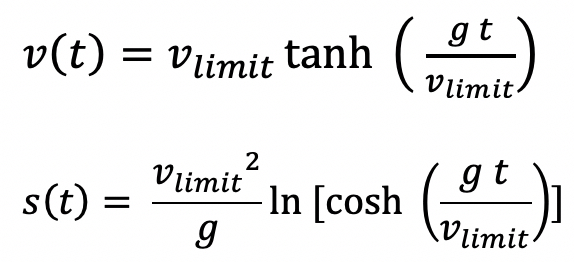 The drag coefficient cD
is a function of the non-dimensional
Reynolds number Re, defined by
>>In theory, the flow is laminar when Reynolds number is below 4,000. However, in practice, turbulence is not effective when Reynolds number is below 200,000; so when the Reynolds number is less than 200,000, you may assume laminar flow. In addition, when the Reynolds number is higher than 2,000,000, you may assume turbulent flow.<< (*). Using a "Height" input the delay due to air resistance is computed (∆t absolute, and ∆t/T in relation to the time T of free fall). Ferdinand Reich's experiments were performed at a height of 158.5 m using spheres of 4,034 cm diameter and 270,45 g mass. The speed limit 86.3 m/s is not reached. The effect of air resistance on time is ∆T = 5.8676s - 5.6845s = 0.1831s, ∆T/T = 3.22%. 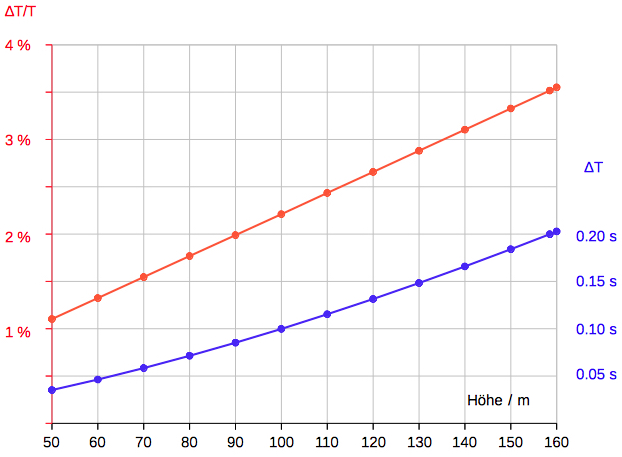 Select "∆t - H": 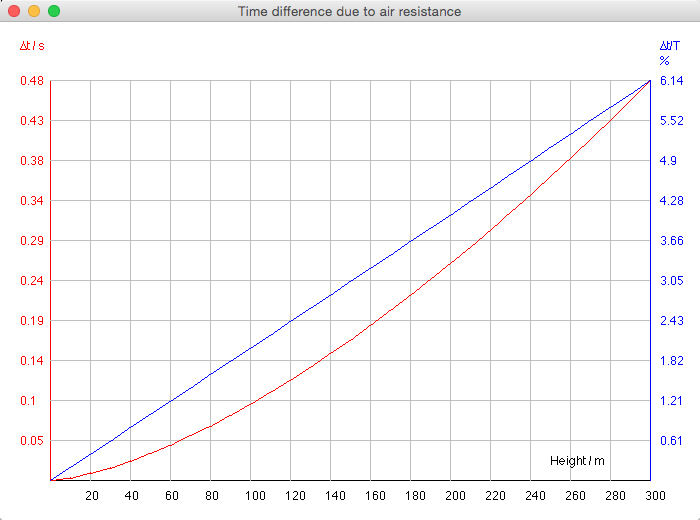 The diagram below is showing
the time difference as a function of
diameter due to air resistance for iron
balls (ρ=7874 kg/m^3) falling from 150 m:
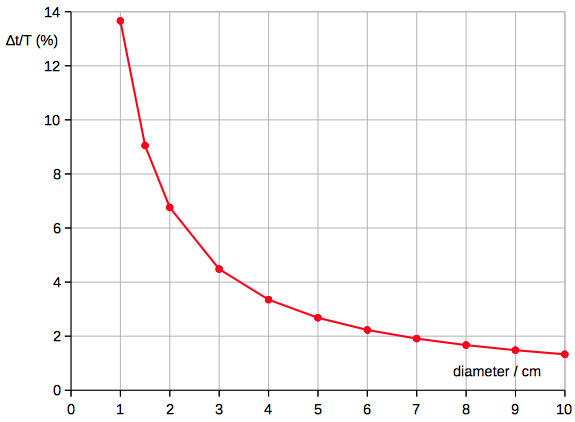 ∆t/T ~ 1/diameter (R2=0.999996) The diagram below is showing
the time difference as a function of mass
due to air resistance for iron balls (ρ=7874
kg/m^3) falling from 150 m:
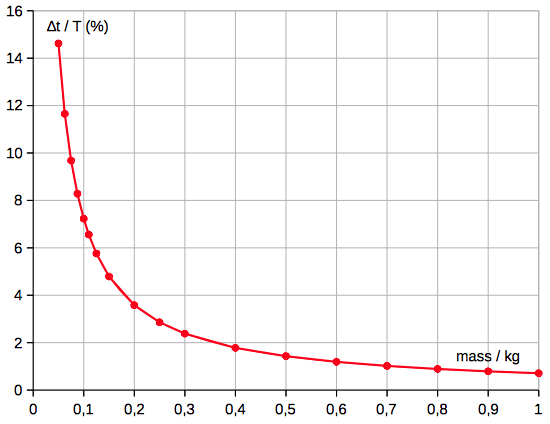 ∆t/T ~
1/mass (R2=0.999992)
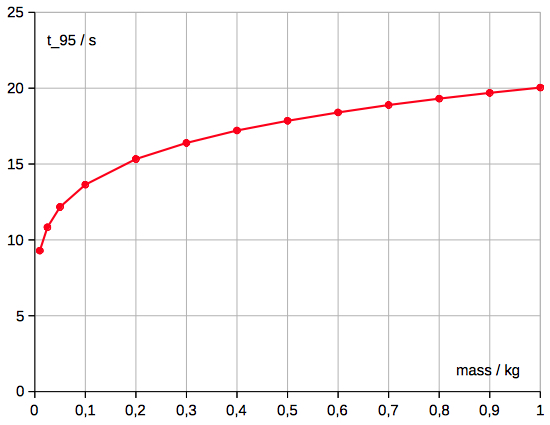
t_95 ~ mass1/6 (R2=0.999997)The time when 95 % of the
terminal velocity (v) is reached as a
function of mass (iron balls) is shown in
the following diagram:
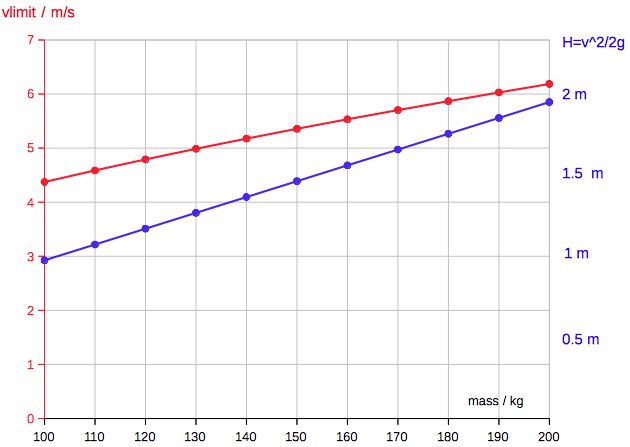
 Parachute The diagram is showing the
rate of descent (vLimit, terminal velocity)
as a function of mass, and the equivalent
height at free fall.
 |
|
|
| Freier
Fall mit und ohne Luftwiderstand
(virtualmaxim) https://www.grc.nasa.gov/www/k-12/airplane/falling.html (*) Drag Force and Drag Coefficient |
2016-2023 J. Giesen
letzte ─nderung: 20.10.2023