Gunter's Quadrant Applet
| Edmund Gunter
(1581-1626), a mathematician and astronomer, first
described his quadrant, a simplified version of the
Arabic astrolabe, in the 1623
publication "De Sectore et Radio". The quadrant
presented here was produced by the eminent instrument
maker Henry Sutton in 1657. It was used to tell the
time of day and to simplify astronomical calculations
for the Sun (altitude, azimuth, declination, right
ascension, position of the Sun in the zodiac). The instrument is equipped with a simple Sun sight on one edge. A weighted thread with a sliding bead is hanging from the apex. |
See
instructions for interactive use below
Quadratum
Horarium Generale (Regiomontanus Dial)
 |
Enter
the year
into text field, and hit "Apply input". (Gregorian Calendar only, later than 1582) |
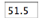 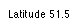 |
Enter
the latitude
(decimal degrees) into the text field, , and hit "Apply input". The latitude is indicated in the lower left. |
 |
The
interactive regions (light gray scales) are changing
the cursor to cross hair. |
 |
Click into the light gray part
of the declination
scale to set the bead (set the date first). |
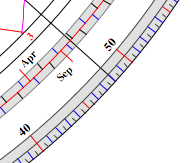 |
Click into the
degree scale (light gray) on the limb to rotate the
thread. |
 |
Use the "Today"
button to set the thread to the current date. The bead
is set to the current Sun's declination. |
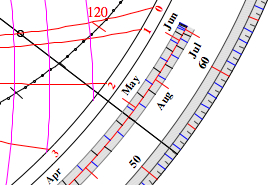 |
- Click into
the light gray calendar (date scale,
inner part for winter
and spring, or outer part for summer and autumn) to
set the thread to the date. - To set the bead to the declination then click within the region of the hour curves on the point where the thread crosses the 12 hours curve. - Then click into the degree scale (light gray) to rotate the thread and the bead. |
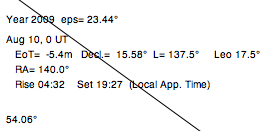 |
Read
the angle,
and the date
within the shadow
square. The values
(for 0 UT) of the
declination, the ecliptic longitude
(and position in the zodiac), the right ascension,
and the times of rise
and set
(local apparent time) are computed and shown within
the shadow square. |
 |
Select
from the "Display Options" menu. |
 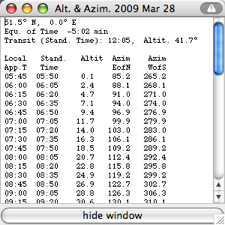 |
Setting
a date will enable the button "Table", which opens a
list of the Local Apparent Time, the Standard Time,
the altitude of the Sun, and the azimuth angle (East
of North, and West of South). |
Thanks to James E. Morrison (Janus) for the
instructions making the Quadrant.
The zodiac and the ecliptic longitude:
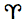 |
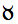 |
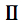 |
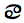 |
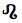 |
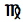 |
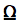 |
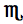 |
 |
 |
 |
 |
| Aries | Taurus | Gemini | Cancer | Leo | Virgo | Libra | Scorpio | Sagittarius | Capricornus | Aquarius | Pisces |
| 0°
- 30° |
30° - 60° | 60° - 90° | 90° - 120° | 120° - 150° | 150° - 180° | 180° - 210° | 210° - 240° | 240° - 270° | 270°
- 300° |
300° - 330° | 330° - 360° |
The zodiac symbols are from the MarVoSym
font, used by the applet.
| J2000 | RA | Declin. | mag | |
| Arcturus |  |
213.92° | 19.18° | -0.05 |
| Aldebaran |  |
69.98° | 16.56° | +0.853 |
| Examples
for use of the digital Gunter Quadrant on 2009, Aug. 10 More Sample Problems in the PDF of James E. Morrison |
|
|
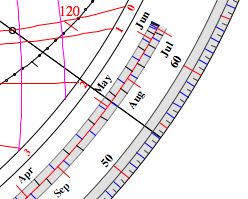
1. Find the declination
of the Sun:
Set the
date and the thread by clicking into the outer
date scale.
Click on the intersection point of the 12 Hours line and the thread to set the bead. Turn the thread to the declination scale by clicking at lower left end of degree scale, and read the declination at the bead: 15.7° (computed: 10.58°) |
  |
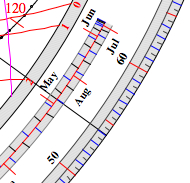
| 2. Find the altitude of the
Sun at local noon: Set the date by
clicking into the outer date scale.
Read the altitude on the degree scale (limb): 54.0° (computed: 53.9°) |
 |
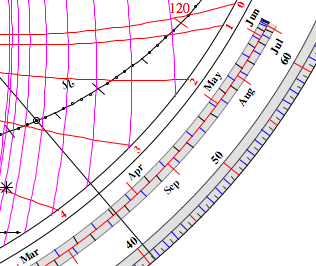
| 3. Find the ecliptic
longitude (position in the zodiac) of the Sun: Set the date
and the thread by clicking into the outer date
scale.
Click on the intersection point of the 12 Hours line and the thread, setting the bead. Turn the bead to the Ecliptic scale by clicking into the degree scale, and read the longitude angle: 137.0°, Leo 17° (computed: 137.5°, Leo 17.5°) |
 |
| 4. Find the Right Ascension
of the Sun: Set the thread
to the longitude of the sun on the ecliptic (see ex.
3, 137°).
Read the angle on the degree scale (limb): 40.5° The Right Ascension is 180°-40.5°= 139.5° (computed: 140.0°) |
 |
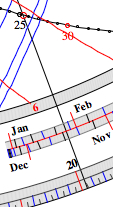
| 5. Find the time of
sunrise: Set the thread
to the date. Click on the
intersection point of the 12 Hours line and the
thread to set the bead. Rotate the
bead to the horizon line, and read the angle on the
degee scale (limb): 20.6°
This angle corresponds to 4*20.6 min = 82.4 min. Subtract (as the date is in summer) this time from 6:00 hours to get 4:38 (computed: 4:32) |
 |
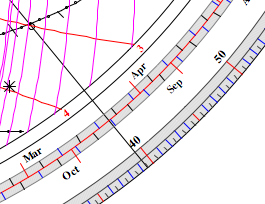
| 6.1 Find the altitude at 3
PM: Set the thread
to the date. Click on the
intersection point of the 12 Hours line and the
thread to set the bead. Rotate the
bead to 3 Hours line, and read the altitude angle on
the degee scale (limb): 39.4°
(computed: 39.2°) |
 |
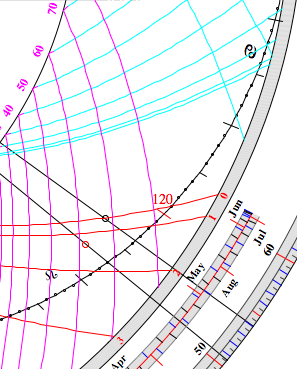
| 6.2 Find the azimuth at 3
PM: Now turn the thread to the co-altitude 90°-39.4°=50.6°, and read the azimuth angle from the azimuth curves using the bead between the 60° and 70° curve: 62° (North of South). (computed: 61.6°) |
 |
My prototype of
Gunter's quadrant, set to Aug.10:


Under construction!
| Books |
| Morrison,
James E.: The Astrolabe, Janus. Softcover edition,
2007, Rehobot Beach, DE USA, ISBN-10: 0939320304, ISBN-13: 978-0939320301. Details... D'Hollander, Raymond: L'Astrolabe. Histoire, theorie et pratique. Institut océanographique, Paris, 1999. ISBN 2-903581-19-3. Hügin, Johannes: Das Astrolabium und die Uhr, Ulm, 1978, ISBN 3-921348-23-4. Stautz, Burkhard: Die Astrolabiensammlung des Deutschen Museums und des Bayerischen Nationalmuseums, Oldenbourg, München 1999. Rohr, René R. J.: Die Sonnenuhr. Geschichte, Theorie, Funktion. Callwey, München 1982. Meyer, Jörg: Die Sonnenuhr und ihre Theorie. Harry Deutsch, Frankfurt 2008. |
|
|
|
The Astrolabe (James E. Morrison) Gunter's
Quadrant
(J. E. Morrison, PDF) Edmund Gunter biography (MacTutor History of Mathematics archive) Gunter's quadrant (Navigation Museum) Gunter quadrant (The Whipple Museum) A Gunter quadrant and practical
knowledge (The Whipple Museum) Gunter quadrant (National Maritime Museum) The
Electric Astrolabe (J. E. Morrison) Astrolabium
(Deutsches Museum) Der
Gunter-Quadrant (Gunter W.) Das
Astrolab (Informatik Uni Erlangen) Keith's Asterolabe (Java applet) Literature on astrolabes (M. Brunold) R.
Doerfler:
The
Analemmas
of
Vitruvius and Ptolemy (PDF) J.
G. Freeman: A Latitude-Independent Sundial
(PDF) F.
A. Stebbins: A Mediaeval Portable Sundial
(PDF)
|
©
2009-2023 J. Giesen
