|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
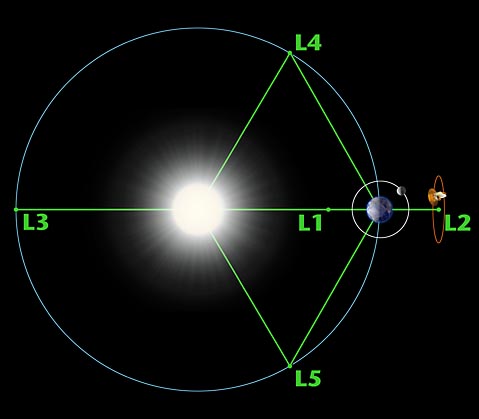
Lagrange Points Applet (1)
| The Lagrangian points are the five
positions in an orbital configuration where a
small object affected only by gravity can
theoretically be stationary relative to two larger
objects (such as a satellite with respect to the
Sun and Earth): |
An article of N. Treitz inspired me to write this applet.
|
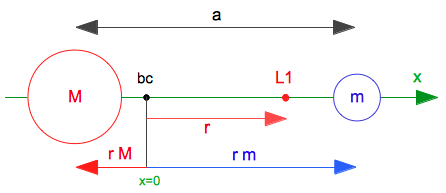
A circular orbit
around the common center of mass bc of the
two bodies is assumed (circular restricted three
body problem). The distance of the bodies M and m
is
a = rM + rm. The barycenter bc of the masses M and m is at distance rM = a·m/(M+m) from the center of M. The three curves of my applet represent the accelerations (positive to the right, negative to the left). At the position x=r of the Lagrange point L1 we have: aM (red) by the mass M (red), at distance r+rM from the center of M |
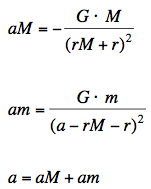
 |
Select from the view options of the menu. |
|
|
You may use the key
"r", or "R" (shift key and "r", faster) to rotate the system around the
center of mass.
|
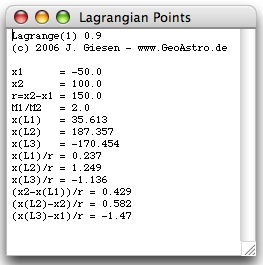
Select "Data Sun-Earth" from the menu:
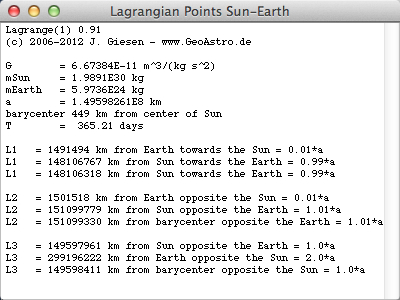
The solutions of my simple iteration method agree within 10-6 % with those by a series (Th. Münch)
Select "Data Earth-Moon" from the menu:
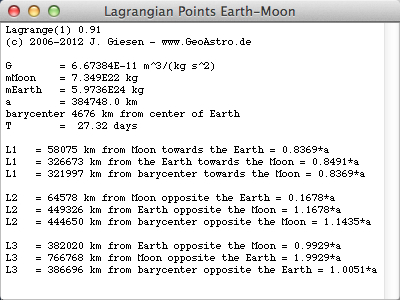
The solutions of my simple iteration method agree within 10-2 % with those by a series (Th. Münch)
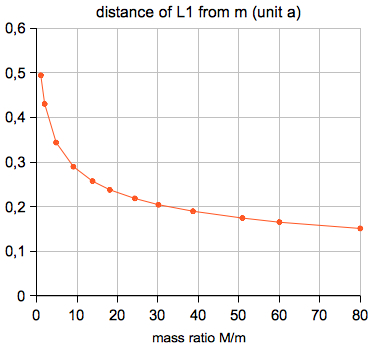
For the Earth-Moon system (M/m=81.3) the point L1 is at a distance of 0.163·a from the Moon
|
|
|
N.
Treitz: am Himmel, Spektrum der
Wissenschaft, Oktober 2006 The Lagrange Points The Lagrangian Points for a Planetary
Orbit Satellite
in
the triangular libration point (example 7) Lagrange
points
for two similar masses Satellites Orrery:
Solar
System Simulator The Lagrange points in the Earth-Moon
system Th. Münch: The
Three-Body Problem and the Lagrangian Points
system |
![]()
Updated:
2023,
Oct 06