|
|
GeoAstro Applets |
Chaos Game |
Java |
Miscel- laneous |
Physics Quiz |
Who is Who ? |
|
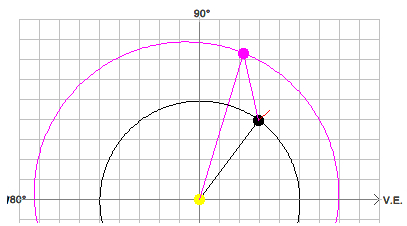
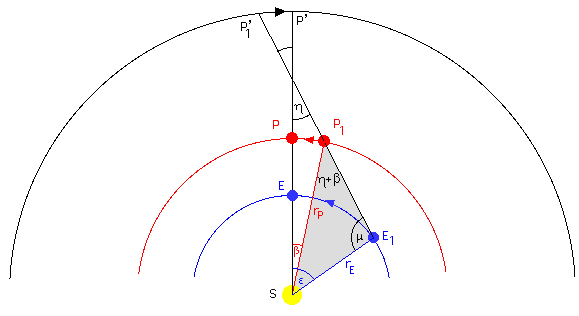
Determining the relative orbital radius of Mars
The opposition of a
planet is a chance to determine its approximate relative orbital radius
by simple observations.
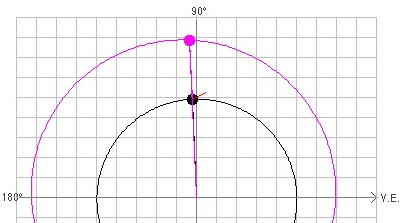
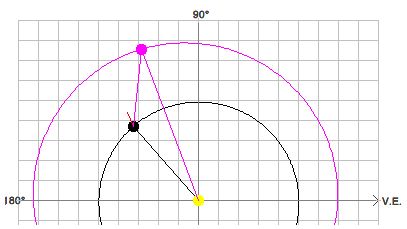
We neglect the inclination of Mars' orbit:
Seen from the Earth against the background stars the line of sight to Mars is turning retrograde from P1' to P by an angle η which can be be measured. Applying the sine rule to the triangle SE1P1 we get: rP / rE
= sin µ / sin(η+β)
and from
(ε-β)
+ µ + (η+β) = 180° = ε + µ + ηwe get
rP
/ rE = sin(η+ε)/sin(η+β)Finally the
orbital radius rP = rMars is given
by:
The angles can
be computed from the sidereal orbital periods of the Earth (365.25 d) and Mars (686.96 d) and the
difference t of time:
ε =
t*360°/365.25 d = t*0.986 °/d
β = t*360°/686.96 d =
t*0.524 °/d
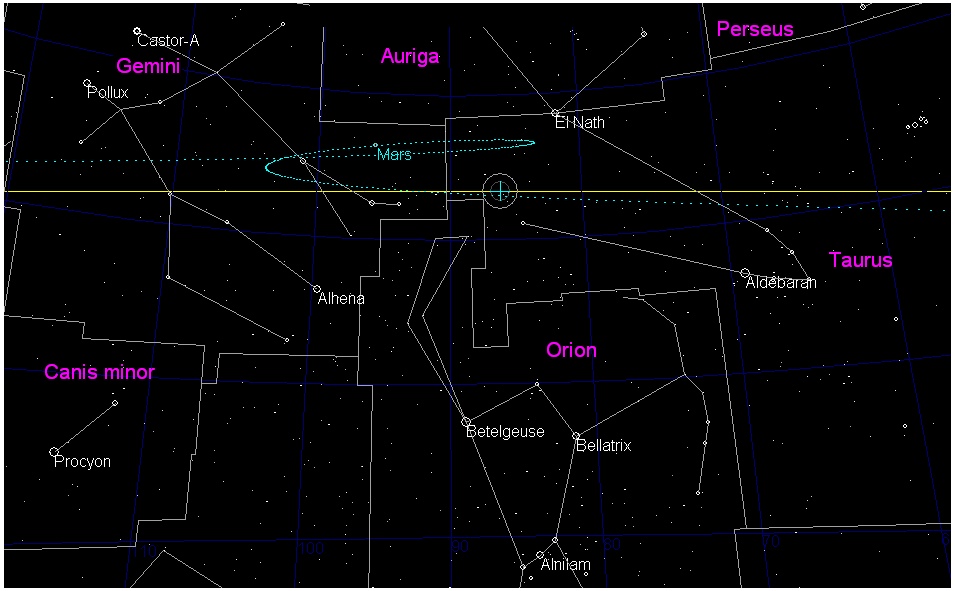
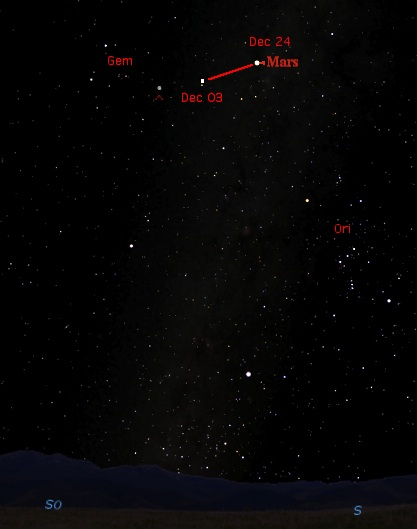
We have to measure the angle η in the sky using photos. Example: 2007 Dec 03, 23 UT to Dec 24, 23 UT: t = 21 d, η = 7.6° |
Updated: 2008, Jan 12