The Dresden Maya Codex
The Dresden Maya Codex from about 1200 to
1250 is one of the very few written documents of the
pre-Columbian Maya culture that have survived to the
present day. It contains 3 astronomical tables:
The Maya calendric system consits of:
A Calendar Round is a combination of the Haab and the Tzolkin. The total number of combinations is 365 Haab days x 260 Tzolkin days =
94,900 days. But the two calendars repeat after 52 Haab years of 365 days, because of the same number of days as in 73 Tzolkin years of 260 days: 52 · 365 = 73 · 260 = 18,980 = 94,900 : 5 Not every possible combination of Tzolkin
and Haab can occur, only 1 in 5 combinations are
possible. Venus Tables Venus was of utmost importance for the Mayas,
considered to bring evil and misfortune when appearing
in the morning sky. |

http://www.mexicolore.co.uk/images-ans/ans_38_01_2.jpg
The base of the Mayan number System is 20,
using 18·20=360 in the 3rd to the last digit and
20·360=7200 in the 4th to the last digit: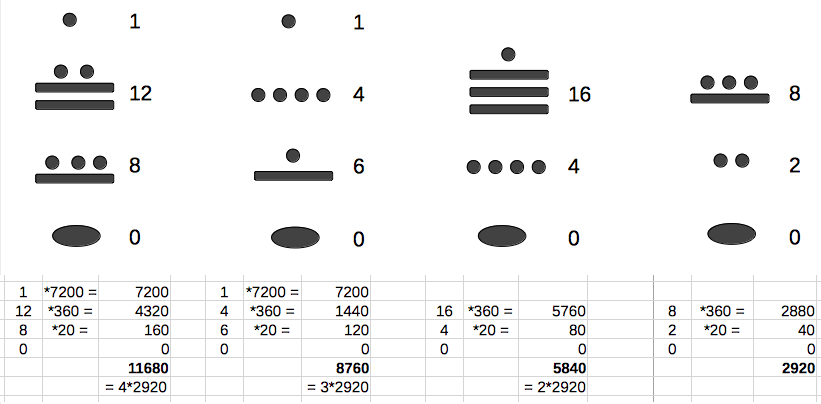 The blue frame:
5 · 2920 = 14600 = 2·7200 + 10·20 = 2.0.10.0 6 · 2920 = 17520 = 2·7200 + 8·360 + 12·20 = 2.8.12.0 7 · 2920 = 20440 = 2·7200 + 16·360 + 14·20 = 2.16.14.0 8 · 2920 = 23360 = 3·7200 + 4·360 + 16·20 = 3.4.16.0 The green frame: 9 · 2920 = 26280 = 3·7200 + 13·20 = 3.13.0.0 10 · 2920 = 29200 = 4·7200 + 1·360 + 2·20 = 4.1.2.0 11 · 2920 = 32120 = 4·7200 + 9·360 + 4·20 = 4.9.4.0 12 · 2920 = 35040 = 4·7200 + 17·360 + 6·20 = 4.17.6.0 The black frame: 13 · 2920 = 37960 = 5·7200 + 5·360 + 8·20 = 5.5.8.0 26 · 2920 = 75920 = 10·7200 + 10·360 + 16·20 = 10.10.16.0 39 · 2920 = 113880 = 15·7200 + 16·360 + 6·20 = 15.16.6.0 52 · 2920 = 151840 = 1·144000 + 1·7200 + 1·360 + 14·20 = 1.1.1.14.0 Between the black and the green frame there are correction numbers, because the exact synodic period of Venus is not 584 days but 593,92 days: a shift of 1 day in 13 cycles. Page 24 is followed by Venus tables on pages 46 to 50, showing certain dates within the 584 days of Venus cycle. On the left of page 46 we find the numbers (orange frame from left to right): 11.16 = 11·20 + 16 = 236
The table starts on the date when Venus vanishes from
the morning sky (invisible at upper conjunction, 236
in the first column on the left).16.6 = 16·20 + 6 = 326, 326 - 236 = 90 1.10.16 = 1·360 + 10·20 + 16· = 576, 576 - 326 = 250 1.11.4 = 1·360 + 11·20 + 4· = 584, 584 - 576 = 8 90 days later Venus becomes visible in the evening sky (326, second column). This period lasts for 250 days, until Venus enters the lower conjunction, being invisible for 8 days. Thereafter the planet reappears as the Morning star in the east. The sum is: 236 + 90 + 250 + 8 = 584.
The dashed red frame on page 46 consists of 4 columns: A. dates when Venus vanishes from the morning sky (invisible for 90 days),In the first line we find the numbers: 3, followed by 2
= (3 + 90) mod 13, followed by 5
= (2+250) mod 13, and 13 = 5 + 8.
The second line (cell A2)
starts using the last number of the preceeding
line (D1):
11 = (13 + 260 - 236)
mod 13= (13 + 24) mod 13 = 11.
The complete table can be computed this way
(if result = number mod 13 = 0 then result =
1).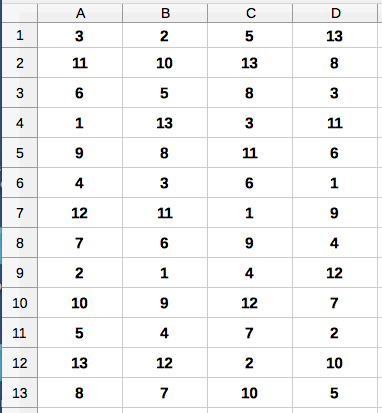 The intervals 90, 250, 8, 236 used in the Tzolkin are only rough approximations to the true periods: 90 days of invisibilty around upper conjunction is far too long, it is only about 50 days (*). The periods as evening and morning star each average about 263 days. So we have: 263 + 50 + 263 + 8 = 584 (**)
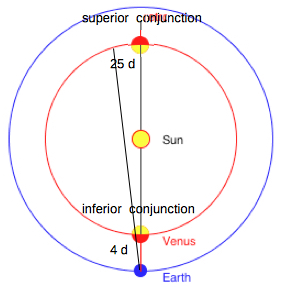 Neglecting the small
eccentricities of the Earth (0.0161) and of Venus
(0.0068) my applet "Geocentric
Motion" is computing the elongation angle
between Venus and the Sun:
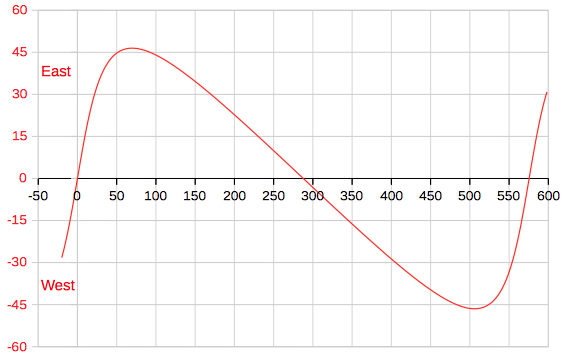 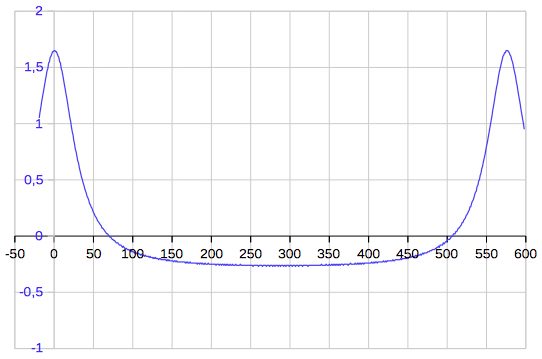 The mean daily change of the
elongation angle is about 1.63° per day around
inferior conjunction, and the elongation
changes from -6,6° to 6.6° within 8 days.
Around superior conjunction (0,162° per day) the elongation takes about 50 days to change from -6.6° to 6.5° degrees. |
Updated: 2015, Feb 14
