|
|
GeoAstro Applets |
Chaos Game |
Java |
Miscel- laneous |
Solar and Lunar Time
| Enter latitude in decimal
degrees: northern latitudes positive, southern negative, and hit RETURN key. Enter longitude in decimal degrees: eastern longitudes positive, western negative, and hit RETURN key. |
|
| Select your time zone: east of Greenwich positive, west of Greenwich negative. |
|
| You may use the keys "h",
"d", "m", "n" to increase the hour, date, month, or
minute, or shift key and "h", "d", "m" , "n" to decrease the hour, date, month, or minute ! Click the applet first !
|
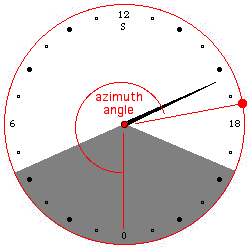
| The Local Solar Time is
12:00 when the Sun crosses the north-south meridian
reaching its highest point in the sky (measured by a
sundial). It differs from local standard time
according to longitude, time zone, and equation of
time. The Local Hour Angle (LHA) of a heavenly body is the angular distance from the observer's meridian to the local meridian of the body, measured on the celestial equator westward from the local meridian through 360°, normally expressed in time-units (h, m, s). Both clocks of my applet are using the local hour angle (of the Sun or the Moon): The clock time is 12:00 at upper transit, and 0:00 at lower transit (minimum altitude). The gray sectors are given by the times of rise and set, also using the local hour angle. A lunar day (also called tidal day) is the time required for the earth to rotate once with respect to the moon, or the interval between two successive upper transits of the Moon over the meridian of a place. The mean lunar day is approximately 24 hours and 50.4 minutes (24.84 solar hours) in length, or 1.035 times as great as the mean solar day. Animation
Conversion
of
standard time to local solar time:
Example: Berlin, time zone UT+1h, longitude 13.41° E, on 2007 Mar 24 at 22:28 standard time (CET). The correction for longitude is 4 minutes per degree of difference between the local longitude (13.41° E) and the longitude of the standard time meridian (UT+1h is corresponding to 15° E): |
| longitude
correction |
equation of time
|
total correction |
standard time | local
solar time |
|
4*(13.41-15) min =
-6.36 min = -6 min 22
s
|
-6 min 16 s
|
-12 min
38 s |
22:28:00 | 22:28:00
- 12 min 38 s = 22:15:22 |
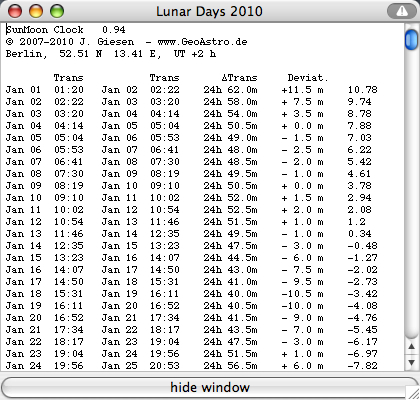
Lunar
days
in 2007: variation between 24 h 38.5 min (Jan 9/10) and 24 h
66.5 min (Nov 25/26)
2007 avarage: 24 h 50.446 min = 24.8408 h
2007-2037 avarage: 24 h 50.471 min = 24.8412 h
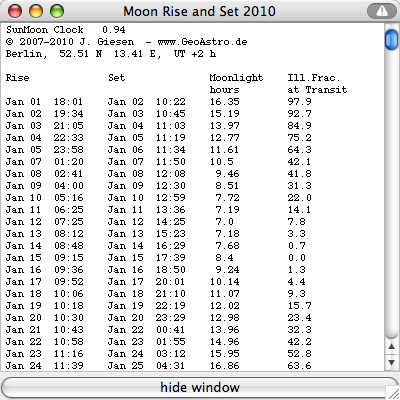
Select
"Rise/Set
Moon" from the "Details" menu:
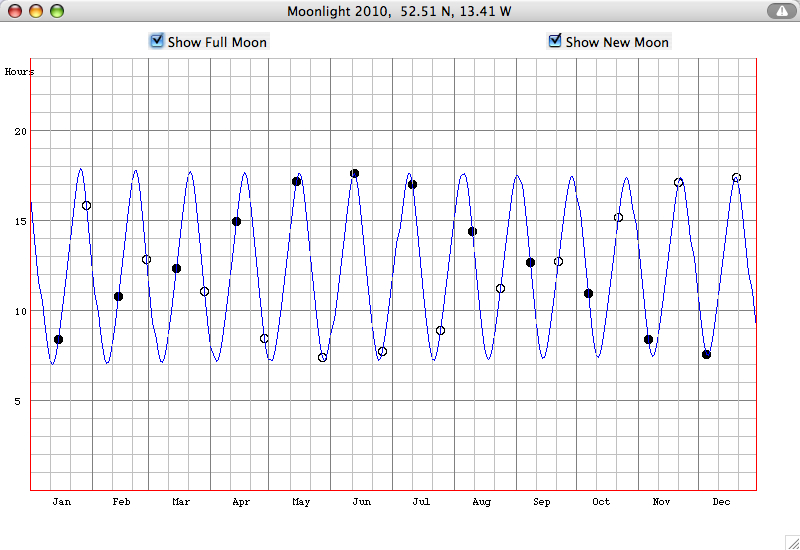
So
far, the Moonlight diagram is not working correctly for high
latitudes > 61.4° = 90° -(23.44°+5.14°),
where the Moon can be visible/unvisible for several
days.
Table:
select
"Lunar Transits" from the "Details" menu.
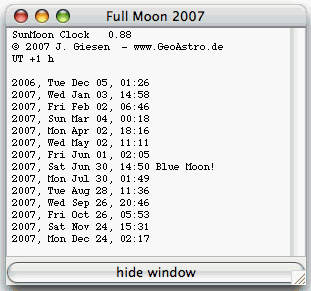
Table: select "Full Moon" from the "Details" menu.
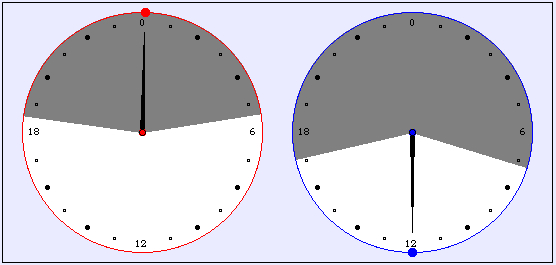
Local upper Moon transit on 2007, Apr 3 at 00:15 local time,
lower transit of The Sun.
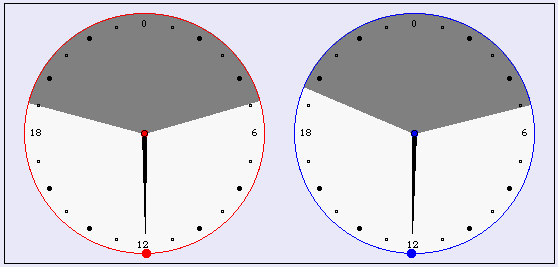
New Moon on 2007, Apr 17 at 11:36 UT
Local upper Moon transit on 2007, Apr 17 at 11:00 UT,
Local upper Sun transit on 2007, Apr 17 at 11:06 UT.
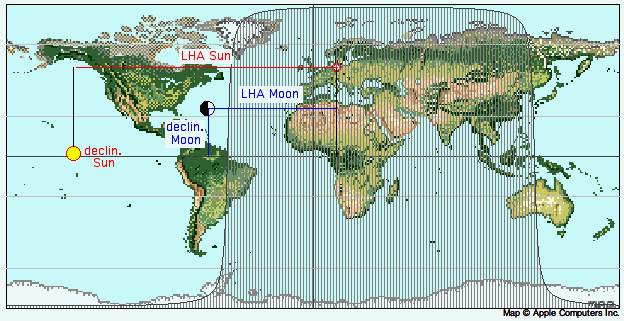
2007 Mar 24 at 21:28 UT
Sun: LHA Berlin = 153.8°, declination = 1.5° N
Moon: LHA Berlin= 75.3°, declination = 28.5° N
|
|
|
Aluna - the
world's first tidal powered Moon Clock Claudius
Franciscus Milliet Dechales: Cursus seu mundus
mathematicus (1674) |
Updated:
2023,
Oct 07