|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Babylonian
Hours, Italian Hours, and Unequal Hours Sundial
Applet
|
|
Enter latitude in decimal degrees (southern negative), then hit the button "Apply input". |
|
|
you may use the keys "h", "d", "m" to increase the hour, date, or month, |
| The
gnomon (length L) of this sundial is vertical. The
shadow of it's top on the horizontal plane indicates the
babylonian hour (and the standard time). Sundials usually show hours starting at midnight. When the Sun culminates (local noon), these dials show 12 p.m. The Babylonian system divides the day into 24 equally long hours beginning at sunrise and ending with the following sunrise. Italian hours begin counting at sunset and ends 24 hours later with the following sunset. The option "Italian Hours 24..0" is counting the hours til sunset. An unequal (seasonal) hour is ne twelfth of the time from sunrise to sunset. As a consequence, hours on summer days are longer than on winter days In this applet the times of sunrise and sunset are for 0° altitude (discarding atmospheric refraction) instead of -0.83°. For low and mid latitudes the difference is only a few minutes. sin h = sin(lat) sin(dec) + cos(lat) cos(dec) cos(H) Setting the altitude h=0: H = arc
cos[-tan(lat) tan(dec)]
|
|||||||||||||||||||||||||||||
The (horizontal) declination lines are drawn for 0° (black), +/- 4°, +/- 8°, +/- 12°, +/- 16°, +/- 20° (gray), and +/- 23.44° (red/blue). Click into the applet area to shift the drawing up or down, and use the "Details" options for scaling. 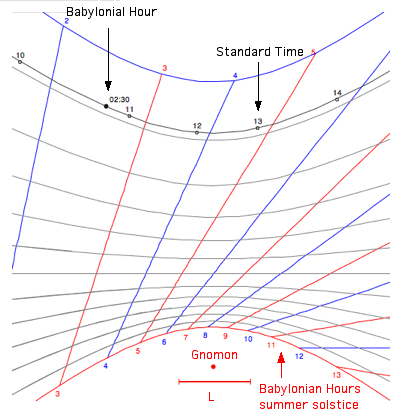 Example:
Berlin (52.52°N, 13.41°E), on Jan 18 at 10:44 Standard Time, which is 2:30 hours after sunrise (8:14), declination -20.5°. |
|
||||||||||||||||||||||||||||

Sunset dial (Italien hours) in a CD box:
Mar 27 at 10:20 CET, about 8.5 hours before sunset.
Select "Zodiac Signs" from the "Details" menu:
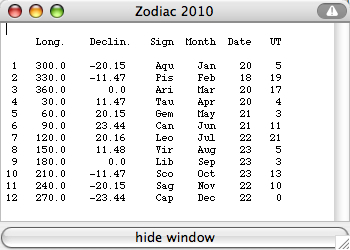
Planetary (Unequal) Hours Clock
More of my sundial applets ...

Santuari de Lluc (Majorca),
2011 Sep 08, 14:08 CEST
The Traditional Roman Breviary:
(Benedict of Nursia, c.480–547)
8 Canonical Hours:
| 1. Matutinum | Midnight (Matins, Vigils, Nocturns) |
| 2. Laudes | Dawn Prayer (Lauds), 3 a.m. |
| 3. Prima | Early Morning Prayer (Prime), 6 a.m. |
| 4. Tertia | Midmorning Prayer (Terce), 9 a.m. |
| 5. Sexta | Midday Prayer (Sext), Noon |
| 6. Nona | Midafternoon Prayer (None), 3 p.m. |
| 7. Vesperae | Evening Prayer (Vespers), 6 p.m. |
| 8. Completae | Night Prayer (Compline), 9 p.m. |
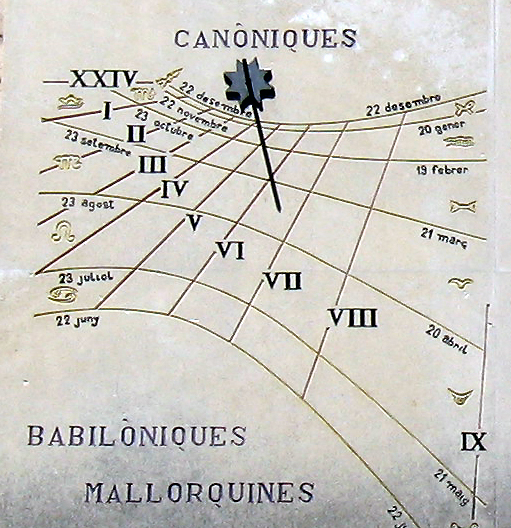
Santuari de Lluc (Majorca), 39.823° N, 2.884° E,
on 2011 Sep 08 at 14:07 CEST
 |
 |
|
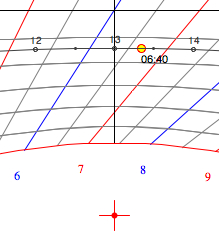
Sundial:
the Babylonian
Hour is 6:40
|
Applet:
the Babylonian
Hour is 6:40
|
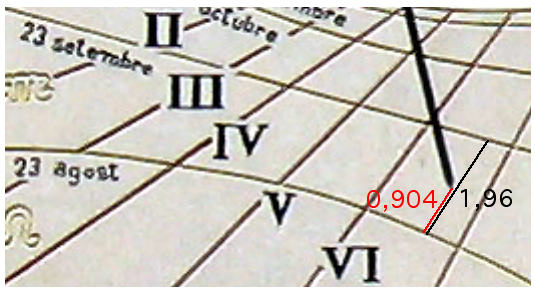
The sundial date
is September 6 (instead
of Sep 8)
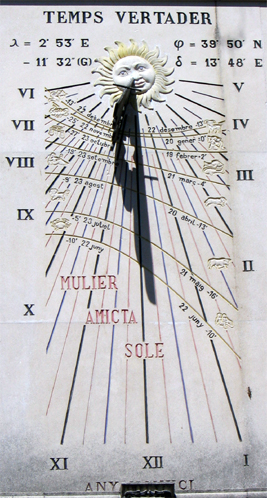
true solar time 12:29
mean local time = true solar time (local apparent time) + 4*(15-λ)m - EoT
EoT=2m 13s, longitude λ =2.884° E
mean local time (CEST) = 12:29 + 4*(15.0-2.884)m - 2.2m + 1h =
12:29 + 48.5m - 2.2m + 1h = 14:15 CEST
my clock was 14:08 CEST
| Books |
| Savoie, Denis: La
Gnomonique, Les Belles Lettres, Paris 2007 |
|
|
|
Liturgy of the Hours (Wikipedia) |
Updated:
2023,
Oct 12
©
2010-2023 J. Giesen
![]()

