Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Physics Quiz

Who is Who ?

Foster-Lambert Sundial Applet

The movable gnomon is directed exactly halfway between the celestial pole and the zenith, producing a circular ring of equiangular hour points. This feature was discovered and published in 1654 by Samuel Foster, and rediscovered by Johann-Heinrich Lambert in 1777. The position of the gnomon is indicated by a blue dot: Check the box "Draw" of the applet to draw the construction of the dial: 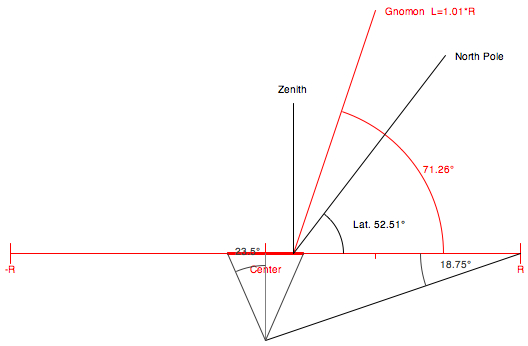Latitude 52.51° N (Berlin) The angle between the gnomon and the horizontal plane is (latitude φ): (90°+φ)/2 The minimum length of the gnomon is (Radius R): R*cos(φ-23.44°)/[cos(23.44°)*cos(0.5*(90°-φ))] On the north-south axis the displacement of the gnomon from the center depends on the declination δ and the latitude φ: R*tan(0.5*(90°-φ))*tan(δ) At noon on the day of summer solstice (winter solstice for the southern hemisphere) the shadow of the top of the gnomon lies on the radius (elevation angle 90°-φ+23.44):

	Enter latitude in decimal degrees and press return key,   enter longitude in decimal degrees and press return key.
	Select "Solar Time" or "Standard Time" from the menu. Chosing "Standard Time" the circle of the hour points will by rotated by an angle determined by the longitude and the current equation of time.
	You may use the keys "y", "m", "d", "h", "n" to increase the year, month, date, hour, or minute, or Shift key and "y", "m", "d", "h", "n" to decreaseyear, month, date, hour, or minute ! Click the applet first !

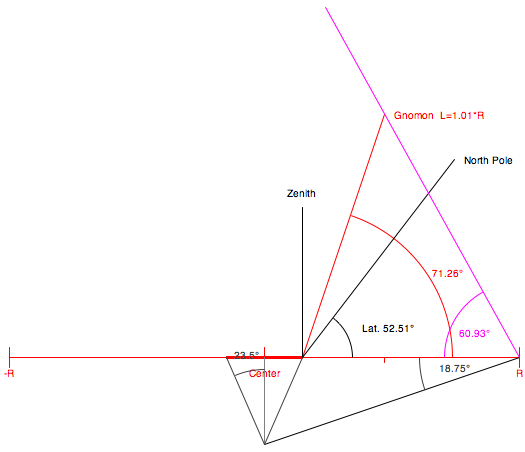
A second gnomon (perpendicular to the first) may be added, checking the box: 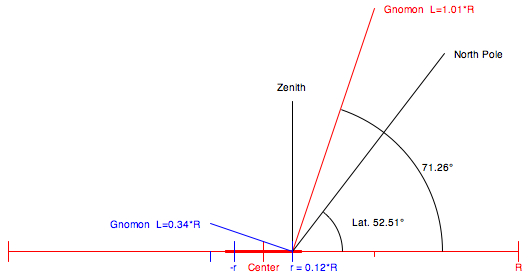The double gnomon mode is implemented for solar time only. For high latitudes the corresponding inner circle of the hour points will be very small. φ = 30°: r = 0.33*R φ = 40°: r = 0.22*R φ = 50°: r = 0.13*R φ = 55°: r = 0.10*R The double gnomon sundial is self-aligning, rotating it until both scales indicate the same time.

Updated: 2010, Aug 2

© 2010 J. Giesen