|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Azimuthal
Orthographic Sundial Applet
|
|
Enter latitude in decimal degrees and press return key, |
 |
Select "Solar
Time" or "Standard Time" from the menu. Chosing "Standard Time" the circle of the hour points will by rotated by an angle determined by the longitude and the current equation of time. |
  |
You may use the keys "y", "m", "d", "h",
"n" to increase
the year, month, date, hour, or minute, Click
the applet first !
|
My Sundial Applet Collection
| The fixed
gnomon of this sundial is perpendicular to the
horizontal dial plane. Orthographic projection of the Sun (declination δ, hour angle H, latitude φ): x
= R*sin(H)*cos(δ)
y
= R*[sin(φ)*cos(δ)*cos(H)
- cos(φ)*sin(δ)]
The declination lines are ellipses, the semi-major axis a=R*cos(δ) being parallel to the east-west direction, and the small semi-axis b=R*sin(φ)*cos(δ) parallel to the north-south direction. The displacement of the declination ellipse from the center is y=R*sin(δ)*cos(φ): 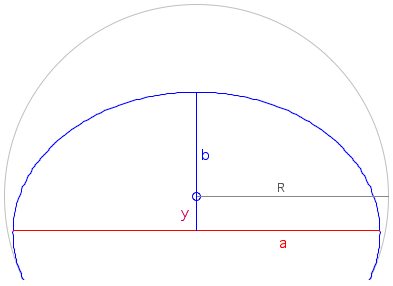 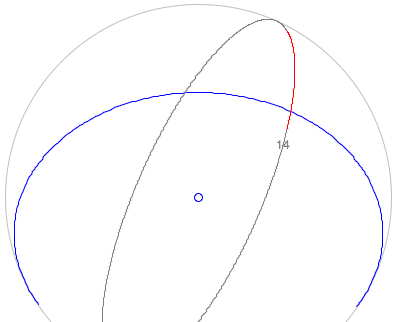 The
declination
ellipse δ=0° (blue) and the hour
ellipse for 6h/18h are touching at the points
east and west:
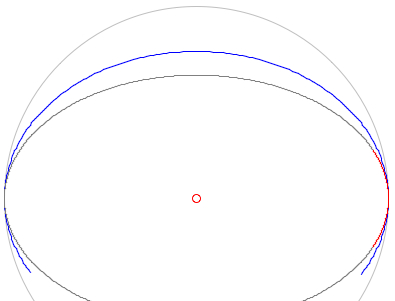  At
local
noon the altitude of the Sun (declination δ) at latitude φ is:
α
= 90° - φ + δ
Latitude φ=50°:The
projection
to the horizon plane:
y = R*cos(α)=R*sin(φ + δ)
summer
solstice:
δ=23.5°,
α=63.5°
y/R=0.96
equinox: δ=0°, α=40° y/R=0.77 winter solstice: δ=-23.5°, α=16.5° y/R=0.45  L
= R*cos(φ-23.5°)
The time is indicated by the intersection of the gnomon shadow with the black declination line. |
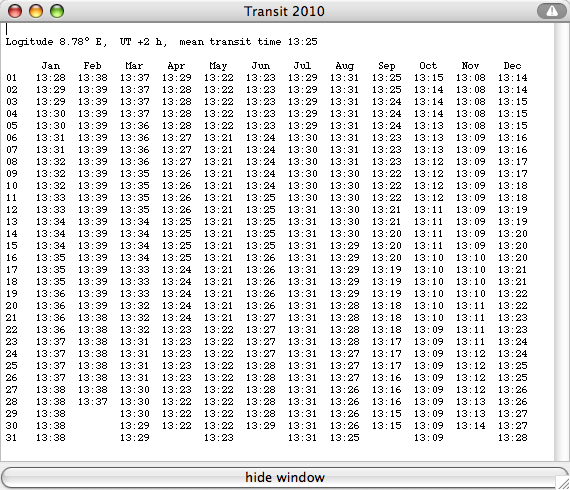
Select "Transit Table" from the "Details" menu:
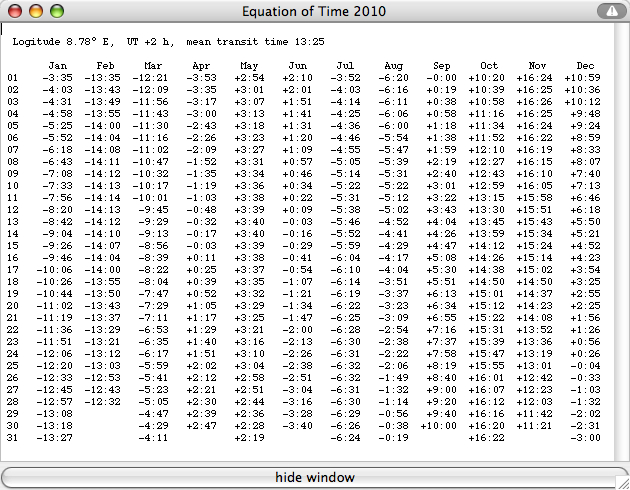
Select "EoT Table" from the "Details" menu:
The sundial in action: Aug 7 at 10:00 solar time (11:31 CEST):

"persex sundialblock" (5x5x2cm), designed for the Netherlands (52°N, 5° E):
Webshop Analemma Sundials, NL :

| Books |
| Denis Savoie: La
Gnomonique, Les Belles Lettres, Paris 2007; p
201-203. |
|
|
|
Orthographic
projection (Wikipedia) C. Macrez:
Cadrans Solaires d'Azimut - Projection
Orthographique et Stéreographique |
Updated:
2023, Oct 06
©
2010-2023 J. Giesen
![]()


