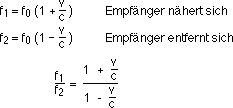Home Site Map Suchen

GeoAstro Applets

Astronomie

Chaos Spiel

Java

Diverses

Physik Quiz

Wer ist es ?

Astrophysik    Weltall Doppler-Effekt Der akustische Dopplereffekt ist allgemein bekannt: beim Vorbeifahren eines Fahrzeugs ändert sich die Tonhöhe: Fahrzeug (41 kB) Der Doppler-Effekt wurde aber nicht im Schallbereich sondern im optischen Bereich entdeckt. Christian Doppler versuchte 1842/43 die Farben der Sterne dadurch zu erklären, dass ihre Eigenbewegung Einfluss auf das wahrgenommene Licht hat. Obwohl diese Annahme nicht zutrifft, war sein Ergebnis richtig, dass bei sich fortbewegenden Sternen die Spektrallinien nach Rot und bei sich nähernden Sternen nach Blau verschoben werden. Seine Folgerungen für den Bereich der Akustik konnte er experimentell bestätigen. © Copyright by Verlag Christian Brandstätter, Wien. 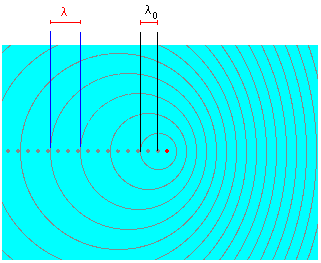Christian Doppler (1803 - 1853) Doppler, Christian Ein Genie hat Geburtstag (Rudolf Kippenhahn, PDF) Der Doppler-Effekt Zusatzinformation für Lehrer, PDF  Doppler-Applet (Autor: Fu-Kwun Hwang) Wenn man die Wellenlängen oder Frequenzen berechnen will, muss man unterscheiden, ob sich die Quelle bewegt und der Empfänger ruht oder ob sich der Empfänger bei ruhender Quelle bewegt. 1. Bewegte Quelle und ruhender Empfänger   Eine Quelle (rot) bewegt sich mit der Geschwindigkeit v nach rechts und sendet Wellen mit der Wellenlänge λ aus, die sich mit der Geschwindigkeit c ausbreiten.  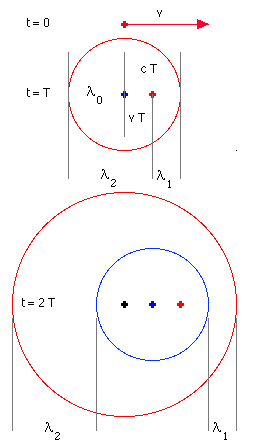Nach einer Periodendauer T hat sich die (rote) Wellenfront um die Strecke cT ausgebreitet, und die Quelle hat den Weg vT zurückgelegt. Ein Beobachter, dem sich die Welle nähert, registriert eine verkleinerte Wellenlänge. Entfernt sich die Quelle vom Beobachter, registriert dieser eine größere Wellenlänge.  Diese Rechnung gilt für den akustischen Dopplereffekt und für Licht falls v << c. Kuckuck (44 kB) Der Ruf des Kuckucks ist eine absteigende kleine Terz mit dem Frequenzverhältnis f1:f2 = 6:5. Für ein Fahrzeug, das beim Vorbeifahren dieses Frequenzverhältnis erzeugt, gilt: v / c = [f1/f2 - 1] / [f1/f2 + 1] = 1/11 Mit der Schallgeschwindigkeit c=340 m/s erhalten wir für die Geschwindigkeit des Fahrzeugs: v=30,9 m/s = 111 km/h Intervall je 44 kB Frequenz- verhältnis f1: f2 Frequenzen f1und f2 in Hz v / c v / km/h (mit c=340 m/s) Prime 1 : 1 396 0 0 kleine Sekunde 16 : 15 409,2 : 383,6 1/31 39,5 große Sekunde 9 : 8 420,8 : 374 1/17 72 kleine Terz 6 : 5 435,6 : 363 1/11 111 große Terz 5 : 4 444,5 : 356,4 1/9 136 Quart 4 : 3 462 : 346,5 1/7 175 Quint 3 : 2 495 : 330 1/5 245 kleine Sexte 8 : 5 514,8 : 321,8 3/13 282 große Sexte 5 : 3 528 : 316,8 1/4 306 kleine Septime 9 : 5 554,4 : 308 2/7 350 große Septime 15 : 8 569,3 : 303,6 7/23 373 Oktave 2 : 1 594 : 297 1/3 408 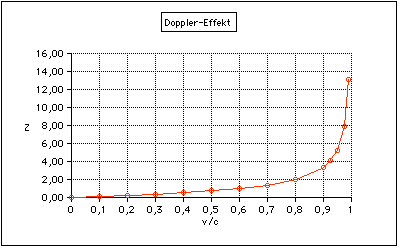Das folgende Diagram zeigt die den Intervallen zugeordneten Frequenzverhältnisse und die jeweils erforderliche Geschwindigkeit der Quelle: 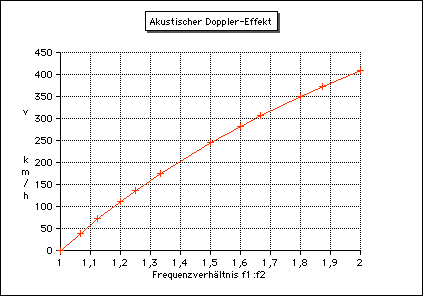Die Aufspaltung der Frequenz fo in die Frequenzen f1 und f2 wächst nichtlinear mit der Geschwindigkeit der Quelle: 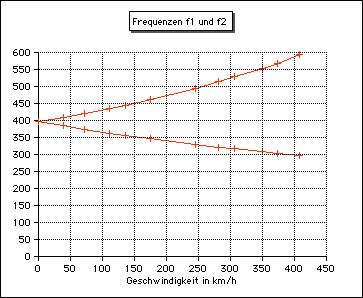  2. Bewegter Empfänger und ruhende Quelle   Befindet sich die Quelle in Ruhe und bewegt sich der Empfänger durch das Medium, dann ändert sich die Wellenlänge nicht, wohl aber die Frequenz der vom Empfänger registrierten Wellen. Sie ist erhöht, wenn sich der Empfänger auf die Quelle zubewegt, und verringert, wenn er sich von ihr entfernt. 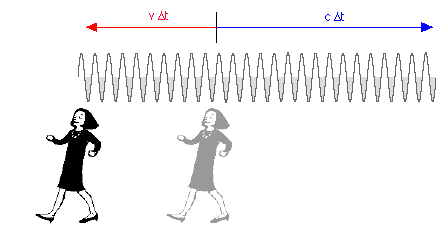In der Zeit Δt passieren den ruhenden Beobachter alle Wellen, die auf der Strecke c Δt zu finden sind. Ihre Anzahl beträgt: c Δt / λ Bewgt sich der Empfänger mit der Geschwindigkeit v auf die Quelle zu, so passiert er zusätzlich v Δt / λ Wellenzüge. Insgesamt beträgt also die Anzahl, die den Empfänger in der Zeit Δt treffen: n = (v Δt + c Δt) / λ Für die Frequenz gilt also: f1 = n /Δt = (v + c) / λ   Intervall Frequenz- verhältnis f1: f2 Frequenzen in Hz v / c v / km/h (mit c=340 m/s) Prime 1 : 1 396 0 0 kleine Sekunde 16 : 15 408,8 : 383,2 1/31 39,5 große Sekunde 9 : 8 419,2 : 372,7 1/17 72 kleine Terz 6 : 5 432 : 360 1/11 111 große Terz 5 : 4 440 : 352 1/9 136 Quart 4 : 3 452,6 : 339,4 1/7 175 Quint 3 : 2 475,2 : 316,8 1/5 245 kleine Sexte 8 : 5 487,4 : 304,6 3/13 282 große Sexte 5 : 3 495 : 297 1/4 306 kleine Septime 9 : 5 509,1 : 282,9 2/7 350 große Septime 15 : 8 516,5 : 275,5 7/23 373 Oktave 2 : 1 528 : 264 1/3 408   Die Aufspaltung der Frequenz fo in die Frequenzen f1 und f2 wächst nichtlinear mit der Geschwindigkeit des Empfängers: 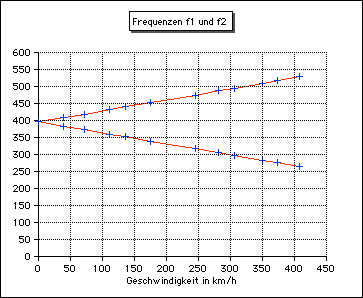Die Überlagerung der beiden Diagramme: 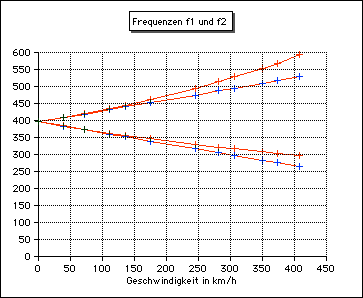Um die Geschwindigkeit v der Quelle zu bestimmen, muss man also messen 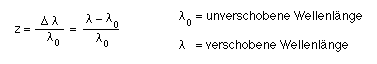3. Optischer Doppler-Effekt  Beim optischen Doppler-Effekt entfällt der Unterschied zwischen bewegter Quelle und bewegtem Empfänger. Hier ergibt sich unter Berücksichtigung der Zeitdilatation die relativistische Formel: 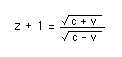v / c 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.95 0.99 z 0.11 0.23 0.36 0.53 0.73 1.00 1.38 2.00 3.36 5.24 13.1   Letzte Änderung: 23.08.2007