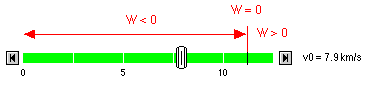|
ist "die Lehre vom Kosmos, seiner allgemeinen Struktur sowie der zeitlichen Änderung dieser Struktur" (Lexikon der Astronomie, Spektrum-Verlag). Eine wichtige Beobachtungsgrundlage für Aussagen über großräumige Bewegungsverhältnisse ist der Hubble-Effekt. Er zeigt eine Expansion des Weltalls, die allgemein akzeptiert wird. Ebenfalls wird akzeptiert, dass die Expansion gebremst erfolgt. Es gibt dann drei Möglichkeiten:
Die Newtonsche Behandlung des expandierenden Weltalls liefert drei Typen von Modellen, deren Eigenschaften überraschenderweise mit denen einer relativistischen Behandlung übereistimmen.
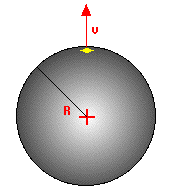
Wir betrachten
eine Galaxis am Rand der kosmischen
Explosionswolke (Radius R), also im
Abstand R vom Zentrum. Die
Gravitationskraft auf der
Kugeloberfläche hängt nur von der Masse
M innerhalb der Kugel ab. Die Gesamtenergie E der Galaxis (Masse m,
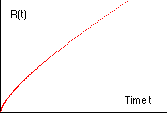
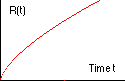
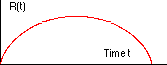
Geschwindigkeit v) setzt sich aus kinetischer Energie Die Gesamtenergie pro Masse (W = E/m) ist: Mit der Gravitationsbeschleunigung g aus mg = G m M / R2 ergibt sich dann: Die Expansion erfolgt genauso wie bei einer Rakete, die mit der Geschwindigkeit v0 senkrecht von der Erdoberfläche (Radius R, Masse M) startet. Die Geschwindigkeit im Abstand r (r > R) ist Die Flugbahn der Rakete hängt von ihrer Gesamtenergie W ab:
Das Applet zeigt die Fälle W<0, W=0 und W>0.
Die Applet-Parameter sind für die Fallbeschleunigung (z.B.: Erde 9,81 m/s2) und Radius (z.B.: Erde 6371 km) vogesehen: <PARAM NAME=gravitation VALUE="9.81">
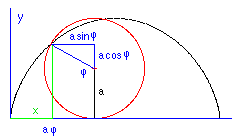
Im Geschwindigkeitsbalken sind die 1. und 2. kosmische Geschwindigkeit markiert (7,91 km/s und 11,2 km/s für die Erde, g=9,81 m/s2, R=6371 km). Die Integration der Differentialgleichung ist nicht ganz trivial. Es ist einfacher, von der Lösung auszugehen und zu zeigen, dass sie der Differentialgleichung genügt (siehe Gehrtsen, Vogel: Physik, Kap. 1.5.9 e9). Falls W<0 ergibt sich für r(t) ein Stück einer Zykloide (wie beim Abrollen eines Kreises mit dem Radius a). Sie besitzt die Parameter-Darstellung: x = a·(phi - sin(phi))
Aus der Energiegleichung ergibt sich Die Zeitfunktionen sind: v(t) = 2/3 p t-1/3
Die Lösung lautet in Parameterdarstellung: t = a (sinh(x) - x) mit den hyperbolischen Funktionen sinh(x) = (ex - e-x)/2 und cosh(x) = (ex + e-x)/2. Die Geschwindigkeit v(t) ist
Aus der Energiegleichung ergibt sich mit dem Hubble-Gesetz v = H R und der mittleren Dichte rho der Universums und seiner Masse M = rho 4 pi R3/3 für den Wert E=0 die kritische Dichte rhoc rhoc = 3 H2/(8 pi G)
Letzte Änderung: 07.10.2023 |