Home Site Map Search

GeoAstro Applets

Astronomy

Chaos Game

Java

Miscel- laneous

Physics Quiz

Who is Who ?

Kepler Applet

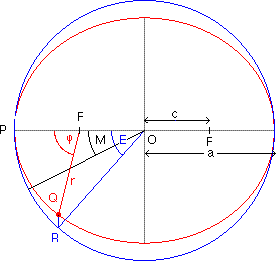
This applet is simulating the elliptical motion of a celestial body.

Use the third scrollbar (blue) to increase uniformly the true anomaly angle phi. Use the fourth scrollbar (red) to increase uniformly the time (mean anomaly M). Select from the menu for details, such as eccentric anomaly. radius, velocity.

F focus P periapsis a = OP semimajor axis e = OF/a = c/a eccentricity Q position of the planet at time t (Q=P for t=0) R point on the auxiliary circle with radius a r = FQ radius vektor E = angle(ROP) eccentric anomaly φ = angle(QFP) true anomaly T orbital period M = t/T*360° = angle(ROP) mean anomaly

The mean anomaly M is the angular distance from perihelion which a (fictitious) planet would have if it moved on the circle of radius a with a constant angular velocity and with the same orbital period T as the real planet moving on the ellipse. By definition, M increases linearly (uniformly) with time.   Choose Show/Hide Velocity v and Show/Hide Vel. Circle: Applet for Mars As the planet P is moving around the ellipse, the end of the velocity vector OP' will move around the gray circle (center M), and FP is always pependicular to to MP'.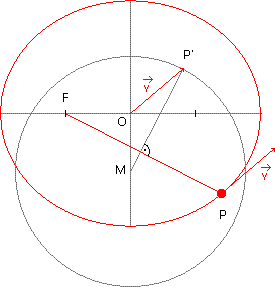

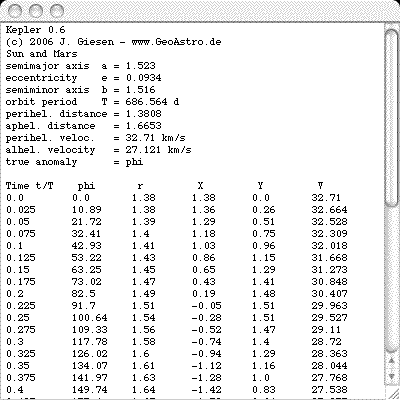
The data window of the applet:

Solving Kepler's equation of elliptical motion

E - e*sin(E) = M(t)

Eccentricity of the orbit of the Earth (long-period variations)

Web Links

Ellipse (MathWorld) Van Schootens Ellipsenzirkel Keplerian problem (Wikipedia) Kepler's Equation (Wikipedia) Solution for the motion as a function of time (Wikipedia) Kepler's Equation of Elliptical Motion Kepler's Equation for Elliptical Motion, a Numerical Solution Utility Resolución de la Ecuación de Kepler Planetary Fact Sheet (NASA)

Updated: 2011, Jun 24