Kepler's Third Law of Planetary Motion:
Johannes
Kepler
announced
his Third Law in his work Harmonices Mundi Libri V,
published in 1619 in Linz, Austria. "Sed
res
est
certissima exactissimaque, quod proportio quae est inter
binorum quorumcunque Planetarum tempora periodica, sit praecise
sesquialtera proportionis mediarum distantiarum, id est Orbium ipsorum." "Am
8.
März
des Jahres 1618, wenn man die genaue Zeitangabe
wünscht, ist sie in meinem Kopf aufgetaucht.. Ich hatte aber keine
glückliche Hand, als ich sie der Rechnung unterzog, und verwarf
sie als falsch. Schließlich kam sie am 15. Mai wieder und
besiegte in einem neuen Anlauf die Finsternis meines Geistes, wobei
sich zwischen meiner siebzehnjährigen Arbeit an den Tychonischen
Beobachtungen und meiner gegenwärtigen Überlegung eine so
treffliche Übereinstimmung ergab, daß ich zunächst
glaubte, ich hätte geträumt und das Gesuchte in den
Beweisunterlagen vorausgesetzt." "Allein
es
ist
ganz sicher und stimmt vollkommen, daß die Proportion, die
zwischen den Umlaufszeiten irgend zweier Planeten besteht, genau das
Anderthalbfache der Proportion der mittleren Abstände, d. h. der
Bahnen selber, ist." Übersetzung: The
ratio
of
the squares of the orbit periods T for two planets is equal to
the ratio of the cubes of their semimajor axes a: a^3/T^2
=
constant The
orbit
period
T for a planet to orbit the sun is proportional to the
semimajor axis a of the ellipse raised to the 3/2 power. The constant
of proportionality is the same for all the planets. T^2 (years^2) versus a^3
(AU^3) logarithmic:

- - sera quidem respexit inertem,
Respexit tamen et longo post tempore venit;
(Vergil, eclogae, I, 27, 29)
Image of that page: Kepler, Johannes. Joannis Kepleri, astronomi Opera omnia .
Volumen V. Page 279
Johannes Kepler: Weltharmonik, Übersetzt und eingeleitet von Max
Caspar, R. Oldenbourg Verlag, München 1997, Seite 291.
(T=orbit period, a=semimajor axis)
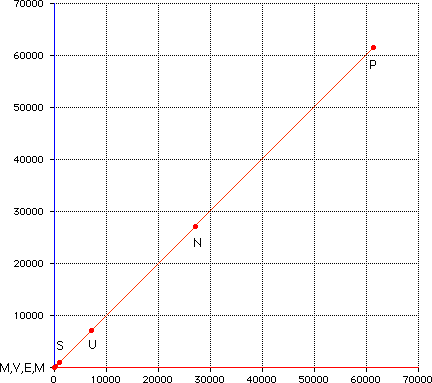
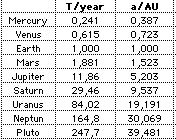
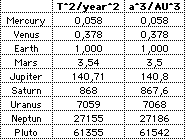
(T=orbit period, a=semimajor axis) 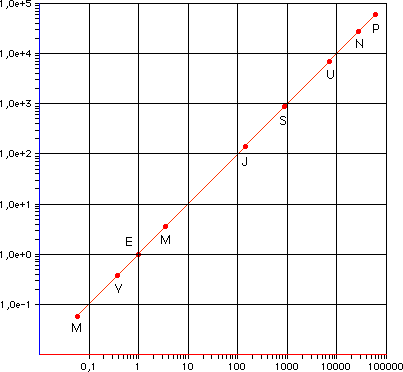
|
|
(c) 2006-2010 J. Giesen
![]()
2010,
Oct
22