|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Prime Vertical Applet
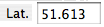 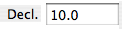 Using the text fields for latitude and declination press "Apply input" after entering the values.  The
items "Derivative" of the Details menu are valid
for a single declination only.
 The
"Draw/Write Time" button will open a diagram
showing the time of the prime vertical
passage. You also may enter the declination
and right ascension of a celestial body to be
observed. Press return key
after entering each value.
δ=7.407° and RA=5.9195h are the coordinates of Betelgeuse (alpha Ori). The prime vertical
is a circle on the celestial sphere passing east
and west through the zenith, and intersecting the
horizon in its east and west points at right
angles. The altitude
and the angle of intersection when passing through
the prime vertical depends on the latitude of the
observer and on the declination of the celestial
body. Example:
eastern prime vertical (azimuth 90°):
Latitude
φ = 50°, declination of the body δ = 40° sin h90 = sin δ / sin
φ = sin 40°/sin 50° = 0.839, h90 = 57.0°
The hour angle ti when crossing the prime vertical: ti = (tan δ / tan φ)*180°/PI, ti = 270° + 40.3° = 310.3° On
the prime vertical the azimuth angle az
increases per minute by:
0.25° * sin φ = 0.192° and
the altitude angle h increases per minute by:
0.25° * cos φ = 0.161° The inversion
point of the path as a function of the hour angle
h=h(t)
 is at
ti=270° at (azi=241.7° | hi=29.5°),
the slope (derivative dh/da) is 43.6°: is at
ti=270° at (azi=241.7° | hi=29.5°),
the slope (derivative dh/da) is 43.6°:sin hi
= sin φ * sin δ =
0.492, hi
= 29.5°
cos azi = sin δ * cos φ / cos hi = 0.475, azi = 241.7° The
inversion point of the path h=h(az)
 is a
different one. is a
different one.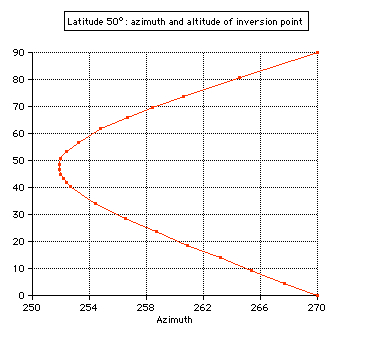 The
parallactic angle q ("angle at the star")
(*)
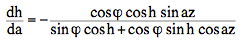 is zero
when the object crosses the meridian, and
largest when passing the point of inversion.
On the prime vertical (az=90°, az=270°) we have the simple equation |dh/da|
= cot φ =
tan (90°-φ)
The formula (*) can be derived using spherical astronomy and calculus: 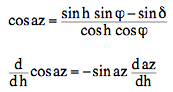 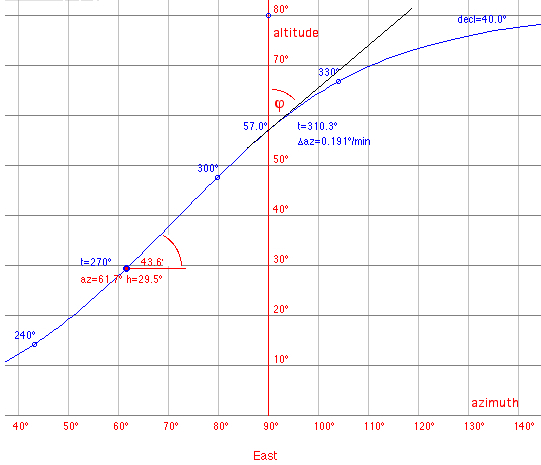 The
body rises at an azimuth angle of az0=180°
(North):
cos az0= - sin δ / cos φ = sin 40°/cos 50° =
1, az0=180°
The diurnal path crosses the horizon at an angle β: tan β = sin az0 / tan φ = 0 / tan φ = 0, β=0°
Objects of declination δ > φ do not pass the prime vertical. Their diurnal path has a point of largest digression (LD) from the meridian where the motion is vertical (parallactic angle 90°). This happens at azimut azLD and hour angle tLD: sin azLD = cos δ / cos φ
cos tLD = tan φ / tan δ Example: φ = 50°, δ = 60°: azLD = 180°+51.1° = 231.1°, tLD = 360°-46.5° = 313.5° 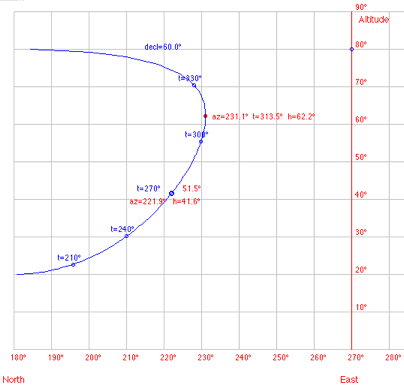 This phenomenon of largest
digression can be used to determine the latitude
of the observer
(W. Embacher).
 51.62° N,
7.96.0° E on 2011 Feb 13 at 21:50 UT:
LST=119.04°
Dubhe, UMa (δ=61.7°):
RA
165.93°, alt.
h=62.1°,
az=229.8°
t = LST - RA = -46.9° There is a (small) difference compared with tLD = arccos(tanφ/tanδ) = 47.2° azLD = arcsin(cos δ/cos φ) = 49.8° (+180° = 229.8°) As already mentioned, the angle between the tangent of the h(az) curve and the prime vertical is equal to the latitude φ of the observer. This method does not require the declination of the star or the time. Using the equation for the differential variation of the altitude h (q=parallactic angle): 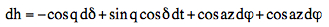 and
setting dδ=0 and
dφ=0:
dh =
sin q cos δ
dt = cos φ
sin az dt
On the prime
vertical (sin az=1):
cos φ = dh/dt
Without a
sextant or a theodolit the
latitude φ can be
determined by observing the
shadow of a vertical gnomon
(length L) pointing exactly
west (or east) which happens
for declination δ>=0° (March 21
until September 23):
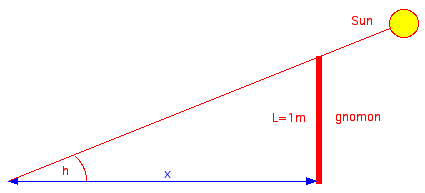 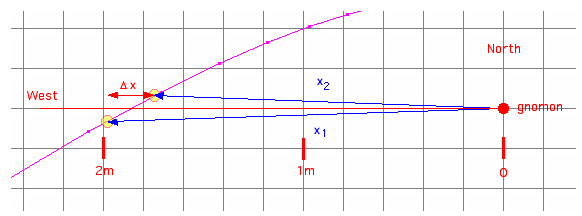 h2
= arctan(L/x2),
h1
= arctan(L/x1),
dh = h2
- h1 =
arctan(L/x2)
- arctan(L/x1),
Simulated example for the Sun: calculated by my Analemma applet, on 2011 June 1: at 7:07 x2= 1.745 m at 7:27 x1= 1.982 m dt = 20 min dh = 29,82° - 26.77° = 3.05° cos φ = dh/dt = 4min/° *
3.05°/20 min = 0.610
φ = 52.4° Location
of
calculation: Berlin φ =
52.51° N (13.41° E)
Date
lines Berlin
(52.51° N)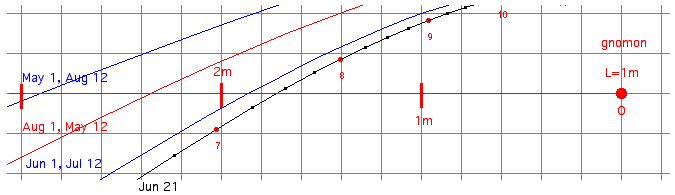
|
Select "Write Table" from the Info menu:
More details:
Sun Azimuth at Rise and Set Applet
Applet: Azimuth, Latitude, Hour
Angle, Declination
of the Sun for various latitudes and dates (equinoxes and solstices).
|
|
|
The measurement by Prestel (using a
Prismenkreis) is accurate to 6''. |
| Books, Articles |
|
Wilfried Kuhn (Hrsg.): Handbuch der
experimentellen Physik Sekundarbereich II, Band 11N:
Astronomie-Astrophysik-Kosmologie, Kapitel 2, Aulis
Verlag, 2011, ISBN 978-3761423967. William Chauvenet: A Manual of Spherical and
Practical Astronomy: Vol. I Spherical Astronomy,
Lippincott, Philadelphia 1891. Wilhelm Embacher: Neue Vorschläge zur
geographischen Ortsbestimmung, Österreichische
Zeitschrift für Vermessungswesen, 1952, Bd. 40, S.
3-88 (3 Teile). |
Updated: 2023, Oct 06