|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Motion of the Moon
Computing
the true longitude of the Moon:
True longitude of Moon = mean longitude + major inequality + evection + variation + annual inequality + reduction to ecliptic + parallactic inequality + more terms
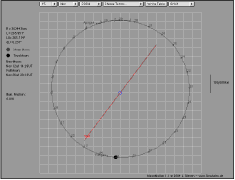
Select "Orbit" instead of "Diagram" to watch the geocentric motion of the Moon.
mean longitude of the Moon: L0 = 218.31617 + 481267.88088*T -
4.06*T*T/3600.0 the Moon's mean anomaly: M = 134.96292 + 477198.86753*T +
33.25*T*T/3600.0 the Sun's mean anomaly: MSun = 357.52543 + 35999.04944*T -
0.58*T*T/3600.0 the mean distance of the Moon from the
ascending node F = 93.27283 + 483202.01873*T -
11.56*T*T/3600.0 the difference between the mean longitudes of
the Sun and the Moon D = 297.85027 + 445267.11135*T -
5.15*T*T/3600.0 Time T = (JD - 2451545)/36525
measured from the mean position of the perigee
Source: Montenbruck, Pfleger: Astronomy on the Personal Computer
True longitude of Moon = mean longitude + major inequality + evection + variation + annual inequality + reduction to ecliptic + parallactic inequality + more terms
L = L0 + ...
(1) Major Inequality (equation of center)
= 22640"*sin(M) + 769*sin(2M) (2) Evection = -4586"*sin(M-2D) (3) Variation = 2370"*sin(2D) (4) Annual Inequality = -668"*sin(MSun) (5) Reduction to the Ecliptic = -412"*sin(2F) (6) Parallactic Inequality = -125"*sin(D) term2 term3 term4 term4 term5 term6 = -212"*sin(2*M-2D) = -206"*sin(M+MSun-2D) = +192"*sin(M+2D) = -165"*sin(MSun-2D) = +148"*sin(L-MSun) = -110"*Math.sin(M+MSun) = - 55"*Math.sin(2F-2D)
(7) More terms
term1
|
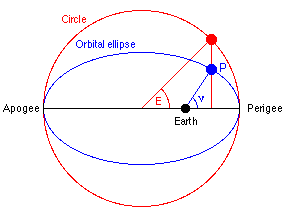
E |
The eccentric anomaly (a parameterization of polar angle) |
|
ν |
The true anomaly specifies the position along the orbit. |
|
M |
The mean anomaly is the angle of the line joining the focus (Earth) to a hypothetical body that has the same orbital period but travels at a uniform angular speed: M = n·(t - T) |
Kepler's Equation for a body orbiting on an ellipse with eccentricity e:
M = E - e·sin(E)
Instructions:
Choose or hide the terms of
interest. The value of a term is red if
active, otherwise black. The values for the annual
inequality, the reduction to the ecliptic, the
parallactic inequality, and the additional terms
are magnified by a factor of 10.
You may use the keys d or m to increase the
date, or month, Click the diagram to get the
coordinates of a point. Click a point and a second point
holding down the Alt key to get a (horizontal)
time intervall. Click a point and a second point
holding down the Shiftkey to get a (vertical)
angular difference. You may use the keys d, m or h to
increase the date, month, or hour,

![]()
![]()
or Shift key and
d or
m to
decrease the date or month !
Click the applet first !

![]()
![]()
![]()
or Shift key and d, m or h to decrease the date,
month, or hour !
Click the applet first !
More applets: More details:
|
|
Last update: 2025, May 29
![]()